题目内容
2. 如图,己知△ABC是等腰直角三角形,AC=BC,∠ACB=90°,AE⊥EF于E,BF⊥EF于F,求证:EF=AE+BF.
如图,己知△ABC是等腰直角三角形,AC=BC,∠ACB=90°,AE⊥EF于E,BF⊥EF于F,求证:EF=AE+BF.
分析 先证△ACE≌△CBF,得出AE=CF,BF=CE,然后自然得证.
解答 证明:∵∠ACB=90°,
∴∠ACE+∠BCF=90°,
∵AE⊥EF于E,
∴∠ACE+∠CAE=90°,
∴∠CAE=∠BCF,
在△ACE和△CBF中,
$\left\{\begin{array}{l}{∠CAE=∠BCF}\\{∠CEA=∠BFC}\\{AB=BC}\end{array}\right.$,
∴△ACE≌△CBF(AAS),
∴CE=BF,AE=CF,
∴EF=CE+CF=AE+BF.
点评 本题主要考查了全等三角形的判定与性质、等腰直角三角形的性质,难度不大,属于基础题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
14.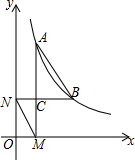 如图,点A、B都在双曲线y=$\frac{k}{x}$的图象上,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN相交于点C,若AB=2MN,点M(1,0),ON=$\frac{3}{2}$,则k的值是( )
如图,点A、B都在双曲线y=$\frac{k}{x}$的图象上,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN相交于点C,若AB=2MN,点M(1,0),ON=$\frac{3}{2}$,则k的值是( )
 如图,点A、B都在双曲线y=$\frac{k}{x}$的图象上,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN相交于点C,若AB=2MN,点M(1,0),ON=$\frac{3}{2}$,则k的值是( )
如图,点A、B都在双曲线y=$\frac{k}{x}$的图象上,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN相交于点C,若AB=2MN,点M(1,0),ON=$\frac{3}{2}$,则k的值是( )| A. | $\frac{3}{2}$ | B. | 2 | C. | 3 | D. | $\frac{9}{2}$ |
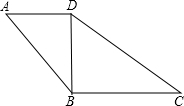 如图,在四边形ABCD中,AD∥BC,∠A=∠BDC.
如图,在四边形ABCD中,AD∥BC,∠A=∠BDC.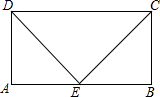 已知:如图,在?ABCD中,E是AB的中点,ED=EC,求证:四边形ABCD是矩形.
已知:如图,在?ABCD中,E是AB的中点,ED=EC,求证:四边形ABCD是矩形.