题目内容
3.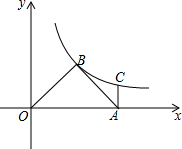 如图,△AOB为等腰三角形,∠ABO=90°,点A为x轴上的点,过点A作AC⊥x轴交双曲线y=$\frac{k}{x}$于C,AC=1,求k的值.
如图,△AOB为等腰三角形,∠ABO=90°,点A为x轴上的点,过点A作AC⊥x轴交双曲线y=$\frac{k}{x}$于C,AC=1,求k的值.
分析 过点B作BD⊥OA于点D,根据△AOB为等腰三角形,∠ABO=90°可得出OD=BD=AD,设BD=a,则OA=2a,故B(a,a),C(2a,1),再由反比例函数图象上点的坐标特点即可得出结论.
解答 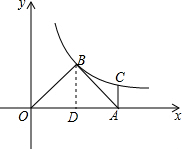 解:过点B作BD⊥OA于点D,
解:过点B作BD⊥OA于点D,
∵△AOB为等腰三角形,∠ABO=90°,AC=1,
∴OD=BD=AD.
设BD=a,则OA=2a,
∴B(a,a),C(2a,1).
∵B、C均在反比例函数y=$\frac{k}{x}$的图象上,
∴a2=2a,解得a=2,
∴k=a2=4.
点评 本题考查的是反比例函数图象上点的坐标特点,根据题意作出辅助线,由等腰直角三角形的性质设出BD的长,用a表示出B、C的坐标是解答此题的关键.

练习册系列答案
相关题目
14.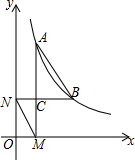 如图,点A、B都在双曲线y=$\frac{k}{x}$的图象上,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN相交于点C,若AB=2MN,点M(1,0),ON=$\frac{3}{2}$,则k的值是( )
如图,点A、B都在双曲线y=$\frac{k}{x}$的图象上,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN相交于点C,若AB=2MN,点M(1,0),ON=$\frac{3}{2}$,则k的值是( )
 如图,点A、B都在双曲线y=$\frac{k}{x}$的图象上,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN相交于点C,若AB=2MN,点M(1,0),ON=$\frac{3}{2}$,则k的值是( )
如图,点A、B都在双曲线y=$\frac{k}{x}$的图象上,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN相交于点C,若AB=2MN,点M(1,0),ON=$\frac{3}{2}$,则k的值是( )| A. | $\frac{3}{2}$ | B. | 2 | C. | 3 | D. | $\frac{9}{2}$ |
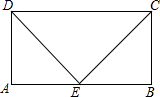 已知:如图,在?ABCD中,E是AB的中点,ED=EC,求证:四边形ABCD是矩形.
已知:如图,在?ABCD中,E是AB的中点,ED=EC,求证:四边形ABCD是矩形.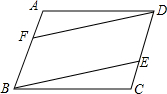 如图,在?ABCD中,点E、F分别在DC、AB上,DC=3CE,BF=2AF,求证:DF=BF,DF∥BF.
如图,在?ABCD中,点E、F分别在DC、AB上,DC=3CE,BF=2AF,求证:DF=BF,DF∥BF.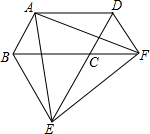 如图,在平行四边形ABCD中,△BCE、△CDF都是等边三角形,试说明△AEF是等边三角形.
如图,在平行四边形ABCD中,△BCE、△CDF都是等边三角形,试说明△AEF是等边三角形.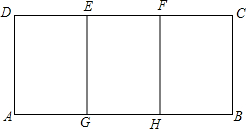 如图,矩形ABCD能分成三个全等的小矩形,且每个小矩形都与矩形ABCD相似,已知AD=1,求AB的长.
如图,矩形ABCD能分成三个全等的小矩形,且每个小矩形都与矩形ABCD相似,已知AD=1,求AB的长.