题目内容
6.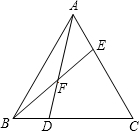 如图,已知△ABC中,AE:EC=1:3,BD:DC=1:2,AD与BE交于点F,求$\frac{EF}{BF}$+$\frac{AF}{DF}$的值.
如图,已知△ABC中,AE:EC=1:3,BD:DC=1:2,AD与BE交于点F,求$\frac{EF}{BF}$+$\frac{AF}{DF}$的值.
分析 作EG∥BC交AD于G,作DH∥AC交BE于H,根据平行线分线段成比例定理分别求出$\frac{EF}{BF}$和$\frac{AF}{DF}$的值,计算即可.
解答 解: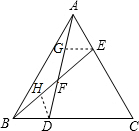 作EG∥BC交AD于G,作DH∥AC交BE于H,
作EG∥BC交AD于G,作DH∥AC交BE于H,
∴$\frac{GE}{CD}$=$\frac{AE}{AC}$=$\frac{1}{4}$,
∵$\frac{BD}{DC}$=$\frac{1}{2}$,
∴$\frac{GE}{BD}$=$\frac{1}{2}$,
∵GE∥BC,
∴$\frac{EF}{FB}$=$\frac{GE}{BD}$=$\frac{1}{2}$,
∵DH∥AC,
∴$\frac{DH}{EC}$=$\frac{BD}{BC}$=$\frac{1}{3}$,
∵$\frac{AE}{EC}$=$\frac{1}{3}$,
∴DH=AE,
∵DH∥AC,
∴$\frac{AF}{FD}$=$\frac{AE}{DH}$=1,
∴$\frac{EF}{BF}$+$\frac{AF}{DF}$=$\frac{1}{2}$+1=$\frac{3}{2}$.
点评 本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
1.下列命题中:
①立方根等于它本身的数有-1,0,1;
②负数没有立方根;
③$\root{3}{6}$=2;
④任何正数都有两个立方根,且它们互为相反数;
⑤平方根等于它本身的数有0和1.
正确的有( )
①立方根等于它本身的数有-1,0,1;
②负数没有立方根;
③$\root{3}{6}$=2;
④任何正数都有两个立方根,且它们互为相反数;
⑤平方根等于它本身的数有0和1.
正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.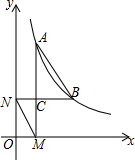 如图,点A、B都在双曲线y=$\frac{k}{x}$的图象上,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN相交于点C,若AB=2MN,点M(1,0),ON=$\frac{3}{2}$,则k的值是( )
如图,点A、B都在双曲线y=$\frac{k}{x}$的图象上,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN相交于点C,若AB=2MN,点M(1,0),ON=$\frac{3}{2}$,则k的值是( )
 如图,点A、B都在双曲线y=$\frac{k}{x}$的图象上,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN相交于点C,若AB=2MN,点M(1,0),ON=$\frac{3}{2}$,则k的值是( )
如图,点A、B都在双曲线y=$\frac{k}{x}$的图象上,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN相交于点C,若AB=2MN,点M(1,0),ON=$\frac{3}{2}$,则k的值是( )| A. | $\frac{3}{2}$ | B. | 2 | C. | 3 | D. | $\frac{9}{2}$ |
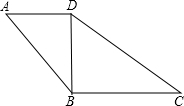 如图,在四边形ABCD中,AD∥BC,∠A=∠BDC.
如图,在四边形ABCD中,AD∥BC,∠A=∠BDC.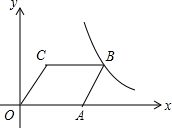 如图,?OABC的边OA在x轴上,C(1,2),A(3,0),双曲线y=$\frac{k}{x}$(x>0)经过点B,求k的值.
如图,?OABC的边OA在x轴上,C(1,2),A(3,0),双曲线y=$\frac{k}{x}$(x>0)经过点B,求k的值.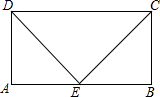 已知:如图,在?ABCD中,E是AB的中点,ED=EC,求证:四边形ABCD是矩形.
已知:如图,在?ABCD中,E是AB的中点,ED=EC,求证:四边形ABCD是矩形.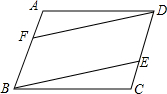 如图,在?ABCD中,点E、F分别在DC、AB上,DC=3CE,BF=2AF,求证:DF=BF,DF∥BF.
如图,在?ABCD中,点E、F分别在DC、AB上,DC=3CE,BF=2AF,求证:DF=BF,DF∥BF.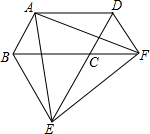 如图,在平行四边形ABCD中,△BCE、△CDF都是等边三角形,试说明△AEF是等边三角形.
如图,在平行四边形ABCD中,△BCE、△CDF都是等边三角形,试说明△AEF是等边三角形.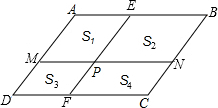 如图,在平行四边形ABCD中.AB∥CD,AD∥BC,P为平行四边形ABCD内一点,过P作EF∥BC,MN∥CD,设四边形AMPE、四边形EPNB、四边形MDFP、四边形CFPN的面积分别为S1、S2、S3、S4.
如图,在平行四边形ABCD中.AB∥CD,AD∥BC,P为平行四边形ABCD内一点,过P作EF∥BC,MN∥CD,设四边形AMPE、四边形EPNB、四边形MDFP、四边形CFPN的面积分别为S1、S2、S3、S4.