题目内容
1.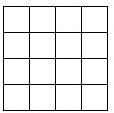 如图,将3枚相同硬币依次放入一个4×4的正方形格子中(每个正方形格子只能放1枚硬币).求所放的3枚硬币中,任意两个都不同行且不同列的概率.
如图,将3枚相同硬币依次放入一个4×4的正方形格子中(每个正方形格子只能放1枚硬币).求所放的3枚硬币中,任意两个都不同行且不同列的概率.
分析 首先分别求得3枚硬币的不同方法,然后利用乘法公式,求得所有等可能的结果;再分别求得任意两个都不同行且不同列的情况,再利用概率公式即可求得答案.
解答 解:计算总的放法数N:第一枚硬币放入16个格子有16种放法;第二枚硬币放入剩下的15个格子有15种放法;第三枚硬币放入剩下的14个格子有14种放法.
∴总的放法数N=16×15×14=3360.
∵计算满足题目要求的放法数m:第一枚硬币放入16个格子有16种放法,与它不同行或不同列的格子有9个.与第一枚硬币不同行或不同列的第二枚硬币有9种放法.与前两枚硬币不同行或不同列的格子有4个,第三枚硬币放入剩下的4个格子有4种放法.
∴满足题目要求的放法数m=16×9×4=576.
∴所求概率P=$\frac{M}{N}$=$\frac{16×9×4}{16×15×14}$=$\frac{6}{35}$.
点评 此题考查了乘法公式的应用.注意分别求得总的放法数与满足题目要求的放法数是关键.

练习册系列答案
相关题目
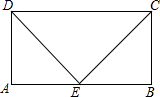 已知:如图,在?ABCD中,E是AB的中点,ED=EC,求证:四边形ABCD是矩形.
已知:如图,在?ABCD中,E是AB的中点,ED=EC,求证:四边形ABCD是矩形.