题目内容
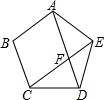 如图,正五边形ABCDE中,对角线AD、CE相交于F,求证:
如图,正五边形ABCDE中,对角线AD、CE相交于F,求证:(1)△AEF是等腰三角形;
(2)四边形ABCE是等腰梯形;
(3)四边形ABCF是菱形.
考点:正多边形和圆
专题:证明题
分析:(1)根据正五边形的性质求出AB=BC=CD=DE=AE,∠BAE=∠AED=∠EDC=∠DCB=∠ABC=108°,再根据等腰三角形的性质求出∠EAD=∠ADE=∠ECD=∠CED=36°,根据三角形内角和定理得出∠AEC的度数,故可得出AE=AF,由此可得出结论;
(2)先根据正五边形的性质求出其内角的度数,再由等腰三角形的性质求出∠DCE的度数,∠BCE的度数,由平行线的判定定理得出AB∥CE,再由AE=BC即可得出结论;
(3)由(1)知,AE=AF,AE=AB,故AB=AF,由(2)知,AB∥CE,∠BCE=∠AFE=72°,所以BC∥AD,由此可得出结论.
(2)先根据正五边形的性质求出其内角的度数,再由等腰三角形的性质求出∠DCE的度数,∠BCE的度数,由平行线的判定定理得出AB∥CE,再由AE=BC即可得出结论;
(3)由(1)知,AE=AF,AE=AB,故AB=AF,由(2)知,AB∥CE,∠BCE=∠AFE=72°,所以BC∥AD,由此可得出结论.
解答:解:(1)∵五边形ABCDE为正五边形,
∴AB=BC=CD=DE=AE,∠BAE=∠AED=∠EDC=∠DCB=∠ABC=108°.
∴∠EAD=∠ADE=∠ECD=∠CED=
=36°,
∴∠AEC=108°-36°=72°,
∴∠AFE=180°-72°-36°=72°,
∴∠AFE=∠AEF,
∴AE=AF,
∴△AEF是等腰三角形;
(2)∵由(1)知,∠ECD=36°,
∴∠BCE=108°-36°=72°.
∵∠B=108°,
∴∠B+∠BCE=180°,
∴AB∥CE.
∵AE=BC,
∴四边形ABCE是等腰梯形;
(3)∵由(1)知,AE=AF,AE=AB,
∴AB=AF.
∵由(2)知,AB∥CE,∠BCE=∠AFE=72°,
∴BC∥AD,
∴四边形ABCF是菱形.
∴AB=BC=CD=DE=AE,∠BAE=∠AED=∠EDC=∠DCB=∠ABC=108°.
∴∠EAD=∠ADE=∠ECD=∠CED=
| 180°-108° |
| 2 |
∴∠AEC=108°-36°=72°,
∴∠AFE=180°-72°-36°=72°,
∴∠AFE=∠AEF,
∴AE=AF,

∴△AEF是等腰三角形;
(2)∵由(1)知,∠ECD=36°,
∴∠BCE=108°-36°=72°.
∵∠B=108°,
∴∠B+∠BCE=180°,
∴AB∥CE.
∵AE=BC,
∴四边形ABCE是等腰梯形;
(3)∵由(1)知,AE=AF,AE=AB,
∴AB=AF.
∵由(2)知,AB∥CE,∠BCE=∠AFE=72°,
∴BC∥AD,
∴四边形ABCF是菱形.
点评:本题考查的是正多边形和圆,熟知正五边形的性质是解答此题的关键.

练习册系列答案
相关题目
当x=2时,代数式ax2+bx3+cx-2的值是2013,则当x=-2时,代数式-ax2+bx3+cx-2的值为( )
| A、-2017 | B、2011 |
| C、-2013 | D、2017 |
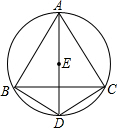 如图,四边形ABDC是圆内接四边形,E是AD上一点,且是△ABC的内心.求证:DB=DE=DC.
如图,四边形ABDC是圆内接四边形,E是AD上一点,且是△ABC的内心.求证:DB=DE=DC. 如图,在Rt△ABC内有矩形PQMN,P、N分别在直角边AB、AC上,Q、M在斜边BC上,已知AB=4,AC=3,内接矩形PQMN的周长等于
如图,在Rt△ABC内有矩形PQMN,P、N分别在直角边AB、AC上,Q、M在斜边BC上,已知AB=4,AC=3,内接矩形PQMN的周长等于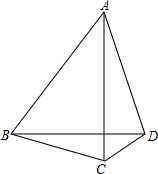 已知:如图,在△ABC中,AB=AC,D是△ABC外一点,且∠ABD=60°,∠ACD=60°.
已知:如图,在△ABC中,AB=AC,D是△ABC外一点,且∠ABD=60°,∠ACD=60°.