题目内容
 如图,等边ABC的边长为3.D,E分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,求AF的长度.
如图,等边ABC的边长为3.D,E分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,求AF的长度.考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:易证△DEF为等边三角形,可得DE=EF=DF,即可证明△AEF≌△BFD,和△AEF≌△CDE,可得AF=BD=CE,BF=AE=CD,即可解题.
解答:解:∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,
∵DE⊥AC,EF⊥AB,FD⊥BC,
∴∠AEF=∠CDE=∠BFD=30°,
∴∠DEF=∠DFE=∠EDF=60°,
∴△DEF为等边三角形,
∴DE=EF=DF,
在△AEF和△BFD中,
,
∴△AEF≌△BFD(AAS),
同理△AEF≌△CDE,
∴△AEF≌△BFD≌△CDE,
∴AF=BD=CE,BF=AE=CD,
∵∠AEF=30°,
∴AE=2AF,
∵AE+AF=AE+CE=AC=3,
∴AF=1.
∴∠A=∠B=∠C=60°,
∵DE⊥AC,EF⊥AB,FD⊥BC,
∴∠AEF=∠CDE=∠BFD=30°,
∴∠DEF=∠DFE=∠EDF=60°,
∴△DEF为等边三角形,
∴DE=EF=DF,
在△AEF和△BFD中,
|
∴△AEF≌△BFD(AAS),
同理△AEF≌△CDE,
∴△AEF≌△BFD≌△CDE,
∴AF=BD=CE,BF=AE=CD,
∵∠AEF=30°,
∴AE=2AF,
∵AE+AF=AE+CE=AC=3,
∴AF=1.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了等边三角形的性质,本题中求证△AEF≌△BFD≌△CDE是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
余姚中学有甲、乙、丙、丁四门选修课,每人每周能选上一周没选的三门课之一,若一同学第一周选修甲,则第五周选修甲的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在Rt△ABC内有矩形PQMN,P、N分别在直角边AB、AC上,Q、M在斜边BC上,已知AB=4,AC=3,内接矩形PQMN的周长等于
如图,在Rt△ABC内有矩形PQMN,P、N分别在直角边AB、AC上,Q、M在斜边BC上,已知AB=4,AC=3,内接矩形PQMN的周长等于 如图,点M(3,m)和点N(2,n)分别在抛物线y=
如图,点M(3,m)和点N(2,n)分别在抛物线y=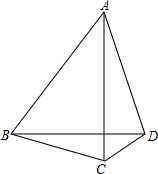 已知:如图,在△ABC中,AB=AC,D是△ABC外一点,且∠ABD=60°,∠ACD=60°.
已知:如图,在△ABC中,AB=AC,D是△ABC外一点,且∠ABD=60°,∠ACD=60°.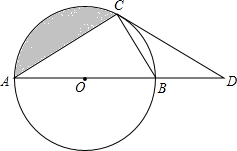 如图,AB是⊙O的直径,C为⊙O上一点,点D在AB的延长线上,∠DCB=∠A.
如图,AB是⊙O的直径,C为⊙O上一点,点D在AB的延长线上,∠DCB=∠A.