题目内容
已知AB是⊙O的直径,点P是AB延长线上的一点,PC切⊙O于点C,PC=3,PA=9,则PB= .
考点:切线的性质
专题:计算题
分析:如图连结OC,设⊙O的半径为r,则OC=r,PO=PA-OA=9-r,根据切线的性质,由PC切⊙O于点C得到OC⊥PC,在Rt△OPC中,利用勾股定理得到r2+32=(9-r)2,解得r=4,然后利用PB=PA-AB进行计算即可.
解答:解:如图, 连结OC,设⊙O的半径为r,则OC=r,PO=PA-OA=9-r,
连结OC,设⊙O的半径为r,则OC=r,PO=PA-OA=9-r,
∵PC切⊙O于点C,
∴OC⊥PC,
在Rt△OPC中,
∵OC2+PC2=PO2,
∴r2+32=(9-r)2,解得r=4,
∴PB=PA-AB=9-8=1.
故答案为1.
 连结OC,设⊙O的半径为r,则OC=r,PO=PA-OA=9-r,
连结OC,设⊙O的半径为r,则OC=r,PO=PA-OA=9-r,∵PC切⊙O于点C,
∴OC⊥PC,
在Rt△OPC中,
∵OC2+PC2=PO2,
∴r2+32=(9-r)2,解得r=4,
∴PB=PA-AB=9-8=1.
故答案为1.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了勾股定理.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
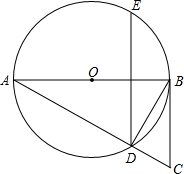 如图,在△ABC中,∠BAC=28°,以AB为直径的⊙O交AC于点D,DE∥CB,连接BD,若添加一个条件,使BC是⊙O的切线,则下列四个条件中不符合的是( )
如图,在△ABC中,∠BAC=28°,以AB为直径的⊙O交AC于点D,DE∥CB,连接BD,若添加一个条件,使BC是⊙O的切线,则下列四个条件中不符合的是( )| A、DE⊥AB |
| B、∠EDB=28° |
| C、∠ADE=∠ABD |
| D、OB=BC |
余姚中学有甲、乙、丙、丁四门选修课,每人每周能选上一周没选的三门课之一,若一同学第一周选修甲,则第五周选修甲的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图为手的示意图,从大拇指开始,按食指,中指,无名指,小指,再回到大拇指的顺序,依次数正整数1,2,3,4,5当数到2015时,对应的手指( )
如图为手的示意图,从大拇指开始,按食指,中指,无名指,小指,再回到大拇指的顺序,依次数正整数1,2,3,4,5当数到2015时,对应的手指( )| A、食指 | B、中指 | C、无名指 | D、小指 |
当x=2时,代数式ax2+bx3+cx-2的值是2013,则当x=-2时,代数式-ax2+bx3+cx-2的值为( )
| A、-2017 | B、2011 |
| C、-2013 | D、2017 |
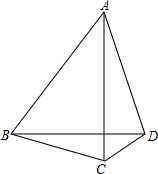 已知:如图,在△ABC中,AB=AC,D是△ABC外一点,且∠ABD=60°,∠ACD=60°.
已知:如图,在△ABC中,AB=AC,D是△ABC外一点,且∠ABD=60°,∠ACD=60°. 如图,在三角形ABC中,点D,E,F分别在BC,AB,AC上,BD=CF,BE=CD,AB=AC,DG⊥EF于点G,求证:EG=FG.
如图,在三角形ABC中,点D,E,F分别在BC,AB,AC上,BD=CF,BE=CD,AB=AC,DG⊥EF于点G,求证:EG=FG.