题目内容
 如图,AB=AC,∠1=∠2,AD=AE,则BD=
如图,AB=AC,∠1=∠2,AD=AE,则BD=考点:全等三角形的判定与性质
专题:
分析:①易证△BAD≌△CAE,可得BD=CE;
②易证∠BAE=∠CAD.
②易证∠BAE=∠CAD.
解答:解:在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE,
∵∠1=∠2,
∴∠1+∠DAE=∠2+∠DAE,即∠BAE=∠CAD.
故答案为 CE,∠CAD.
|
∴△BAD≌△CAE(SAS),
∴BD=CE,
∵∠1=∠2,
∴∠1+∠DAE=∠2+∠DAE,即∠BAE=∠CAD.
故答案为 CE,∠CAD.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△BAD≌△CAE是解题的关键.

练习册系列答案
相关题目
余姚中学有甲、乙、丙、丁四门选修课,每人每周能选上一周没选的三门课之一,若一同学第一周选修甲,则第五周选修甲的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图为手的示意图,从大拇指开始,按食指,中指,无名指,小指,再回到大拇指的顺序,依次数正整数1,2,3,4,5当数到2015时,对应的手指( )
如图为手的示意图,从大拇指开始,按食指,中指,无名指,小指,再回到大拇指的顺序,依次数正整数1,2,3,4,5当数到2015时,对应的手指( )| A、食指 | B、中指 | C、无名指 | D、小指 |
当x=2时,代数式ax2+bx3+cx-2的值是2013,则当x=-2时,代数式-ax2+bx3+cx-2的值为( )
| A、-2017 | B、2011 |
| C、-2013 | D、2017 |
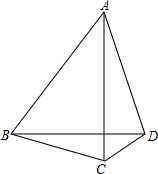 已知:如图,在△ABC中,AB=AC,D是△ABC外一点,且∠ABD=60°,∠ACD=60°.
已知:如图,在△ABC中,AB=AC,D是△ABC外一点,且∠ABD=60°,∠ACD=60°.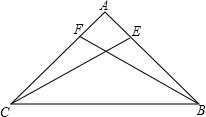 在△ABC中,BE=CF,∠CFB=∠BEC,那么AC=AB,你知道为什么吗?
在△ABC中,BE=CF,∠CFB=∠BEC,那么AC=AB,你知道为什么吗?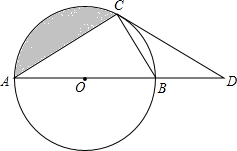 如图,AB是⊙O的直径,C为⊙O上一点,点D在AB的延长线上,∠DCB=∠A.
如图,AB是⊙O的直径,C为⊙O上一点,点D在AB的延长线上,∠DCB=∠A.  已知:如图,在平面直角坐标xOy中,边长为2的等边△OAB的顶点B在第一象限,顶点A在x轴的正半轴上.另一等腰△OCA的顶点C在第四象限,OC=AC,∠C=120°.现有两动点P、Q分别从A、O两点同时出发,点Q以每秒1个单位的速度沿OC向点C运动,点P以每秒3个单位的速度沿A→O→B运动,当其中一个点到达终点时,另一个点也随即停止.
已知:如图,在平面直角坐标xOy中,边长为2的等边△OAB的顶点B在第一象限,顶点A在x轴的正半轴上.另一等腰△OCA的顶点C在第四象限,OC=AC,∠C=120°.现有两动点P、Q分别从A、O两点同时出发,点Q以每秒1个单位的速度沿OC向点C运动,点P以每秒3个单位的速度沿A→O→B运动,当其中一个点到达终点时,另一个点也随即停止.