题目内容
3.下列是某数学兴趣小组的一次探究性话动.
请你根据活动小组的探究方法,探究下列问题:
已知7+$\root{3}{19}$的小数部分是m,11-$\root{3}{19}$的小数部分为n,求m+n.
分析 先根据题意得出$\root{3}{19}$的小数部分,再求和即可.
解答 解:∵8<19<27,
∴2<$\root{3}{19}$<3,
∴9<7+$\root{3}{19}$<10,-3<-$\root{3}{19}$<-2,
∴8<11-$\root{3}{19}$<9,
∴7+$\root{3}{19}$的小数部分m=7+$\root{3}{19}$-9=$\root{3}{19}$-2,11-$\root{3}{19}$的小数部分n=11-$\root{3}{19}$-8=3-$\root{3}{19}$,
∴m+n=$\root{3}{19}$-2+3-$\root{3}{19}$,=1.
点评 本题考查的是估算无理数的大小,先根据题意得出m、n的值是解答此题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
2.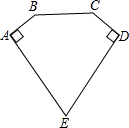 如图,已知AE=DE=5,AB=CD,BC=4,∠E=60°,∠A=∠D=90°,那么五边形ABCDE的面积是( )
如图,已知AE=DE=5,AB=CD,BC=4,∠E=60°,∠A=∠D=90°,那么五边形ABCDE的面积是( )
 如图,已知AE=DE=5,AB=CD,BC=4,∠E=60°,∠A=∠D=90°,那么五边形ABCDE的面积是( )
如图,已知AE=DE=5,AB=CD,BC=4,∠E=60°,∠A=∠D=90°,那么五边形ABCDE的面积是( )| A. | 6$\sqrt{2}$ | B. | 6$\sqrt{3}$ | C. | 7$\sqrt{2}$ | D. | 7$\sqrt{3}$ |
 如图,在平行四边形ABDC中,△EDC是由△ABC绕顶点C旋转40°所得,顶点A恰好转到AB上一点E的位置,则∠1=70度.
如图,在平行四边形ABDC中,△EDC是由△ABC绕顶点C旋转40°所得,顶点A恰好转到AB上一点E的位置,则∠1=70度.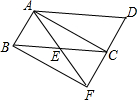 如图,已知点E是?ABCD中BC边的中点,连接AE并延长交DC的延长线于点F.
如图,已知点E是?ABCD中BC边的中点,连接AE并延长交DC的延长线于点F.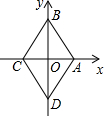 菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,$\sqrt{3}$),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒1个单位长度的速度移动,移动到第2015秒时,点P的坐标为( $\frac{3}{4}$,-$\frac{\sqrt{3}}{4}$).
菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,$\sqrt{3}$),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒1个单位长度的速度移动,移动到第2015秒时,点P的坐标为( $\frac{3}{4}$,-$\frac{\sqrt{3}}{4}$). 已知抛物线y=ax2-4ax+3与x轴交于A(1,0),B,与y轴交于点C.
已知抛物线y=ax2-4ax+3与x轴交于A(1,0),B,与y轴交于点C.