题目内容
6.一列分数有规律地排列如下:$\frac{1}{1}$,$\frac{2}{1}$,$\frac{1}{2}$,$\frac{3}{1}$,$\frac{2}{2}$,$\frac{1}{3}$,$\frac{4}{1}$,$\frac{3}{2}$,$\frac{2}{3}$,$\frac{1}{4}$,$\frac{5}{1}$,$\frac{4}{2}$,$\frac{3}{3}$,$\frac{2}{4}$,$\frac{1}{5}$,…,则第200个分数是$\frac{11}{10}$.分析 观察此数列,将此数列进行分组,第一组有一个数,分子与分母都是1,和为2,;第二组有2个数,分母从1到2,分子从2到1,分子与分母的和为3;第三组有3个数,分母从1到3,分子从3到1,分子与分母的和为4;…那么第n组就有n个数,分母从1到n,分子从n到1,分子与分母的和为n+1;由此即可求出到n组一共有190个数,那第200个数即可知道是多少.
解答 解:∵1+2+3+4+5+…+19=$\frac{19×(1+19)}{2}$=190,200-190=10,
∴第200个分数是第20组的第10个分数,分母是10,分子是11,为$\frac{11}{10}$.
故答案为:$\frac{11}{10}$.
点评 本题考查了规律型:数字的变化类,解答此题的关键是,根据所给数列,找出其规律,再根据规律解答即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
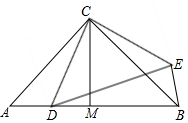 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC=2$\sqrt{2}$,CM⊥AB,垂足为M,点D在边AB上,连接CD,过点C作CE⊥CD,且CE=CD,连接DE、BE.
如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC=2$\sqrt{2}$,CM⊥AB,垂足为M,点D在边AB上,连接CD,过点C作CE⊥CD,且CE=CD,连接DE、BE. 如图,在平行四边形ABDC中,△EDC是由△ABC绕顶点C旋转40°所得,顶点A恰好转到AB上一点E的位置,则∠1=70度.
如图,在平行四边形ABDC中,△EDC是由△ABC绕顶点C旋转40°所得,顶点A恰好转到AB上一点E的位置,则∠1=70度.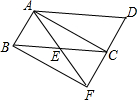 如图,已知点E是?ABCD中BC边的中点,连接AE并延长交DC的延长线于点F.
如图,已知点E是?ABCD中BC边的中点,连接AE并延长交DC的延长线于点F.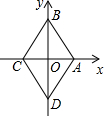 菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,$\sqrt{3}$),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒1个单位长度的速度移动,移动到第2015秒时,点P的坐标为( $\frac{3}{4}$,-$\frac{\sqrt{3}}{4}$).
菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,$\sqrt{3}$),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒1个单位长度的速度移动,移动到第2015秒时,点P的坐标为( $\frac{3}{4}$,-$\frac{\sqrt{3}}{4}$).