a.b.c是同一平面内不重合的三条直线.下列四个命题:①如果a∥b.a⊥c.那么b⊥c,②如果b∥a.c∥a.那么b∥c,③如果b⊥a.c⊥a.那么b⊥c,④如果b⊥a.c⊥a.那么b∥c．其中真命题是①②④ 题目和参考答案——青夏教育精英家教网—

题目内容

15．a、b、c是同一平面内不重合的三条直线，下列四个命题：①如果a∥b，a⊥c，那么b⊥c；②如果b∥a，c∥a，那么b∥c；③如果b⊥a，c⊥a，那么b⊥c；④如果b⊥a，c⊥a，那么b∥c．其中真命题是①②④（填写所有真命题的序号）

分析根据平行线的判定定理与性质对各小题进行逐一分析即可．

解答解：①∵a∥b，a⊥c，∴b⊥c，是真命题；
②∵b∥a，c∥a，∴b∥c，是真命题；
③∵b⊥a，c⊥a，∴b∥c，故原命题是假命题；
④∵b⊥a，c⊥a，∴b∥c，是真命题．
故答案为：①②④．

点评本题考查的是命题与定理，熟知在同一平面内垂直于同一条直线的两条直线互相平行是解答此题的关键．

练习册系列答案

蓝博士暑假作业甘肃少年儿童出版社系列答案

相关题目

20．

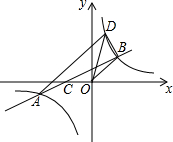如图，点A和点B分别是反比例函数y=$\frac{k}{x}$（k≠0）图象上两点，连接AB交x轴负半轴于点C，连接BO，tan∠BCO=$\frac{1}{2}$，∠BOC=135°，CO=2，过点A作AD∥BO交反比例函数y=$\frac{k}{x}$于点D，连接OD，BD．
（1）求点A的坐标；
（2）求△OBD的面积．

6．阅读下列材料：
据报道，2014年北京市环境空气中PM2.5年平均浓度为85.9微克/立方米．PM2.5一级优天数达到93天，较2013年大幅度增加了22天，PM2.5导致的重污染天数也明显减少，从2013年的58天下降为45天，但严重污染天数增加2天．
2015年北京缓解空气中PM2.5年均浓度为80.6微克/立方米，约为国家标准限值的2.3倍，成为本市大气污染治理的突出问题，市环保局数据显示，2015年本市空气质量达标天数为186天，较2014年增加14天，其中PM2.5一级优的天数增加了13天．
2015年本市PM2.5重污染天数占全年总天数的11.5%，其中在11-12月当中发生重污染22天，占11月和12月天数的36%，与去年同期相比增加15天．
根据以上材料解答下列问题：
（1）2014年本市空气质量达标天数为172天；
PM2.5年平均浓度的国家标准限值是35微克/立方米；（结果保留整数）
（2）选择统计表或统计图，将2013-2015年PM2.5一级优天数的情况表示出来；
（3）小明从报道中发现“2015年11-12月当中发生重污染22天，占11月和12月天数的36%，与去年同期相比增加15天”，他由此推断“2015年全年的PM2.5重污染天数比2014年要多”你同意他的结论吗？并说明理由．

3．

如图，直线a、b被直线c所截，a∥b，∠1=35°，则∠2等于（　　）

10．（1）计算：${（\sqrt{3}-\sqrt{2}）^0}-{（{-\frac{1}{2}}）^{-2}}+|-2|$
（2）化简：$（\frac{m}{m+3}-\frac{2m}{m+3}）÷\frac{m}{{{m^2}-9}}$
（3）解方程：$\frac{x-3}{4-x}-1=\frac{1}{x-4}$．

20．

如图，在△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC的中点，两边PE，PF分别交AB，AC于点E，F，连接EF交AP于点G．给出以下四个结论：①∠B=∠C=45°；②AE=CF；③△EPF是等腰直角三角形；④四边形AEPF的面积是△ABC面积的一半．其中正确的有（　　）

7．一个扇形占其所在圆的面积的$\frac{1}{8}$，则该扇形圆心角是（　　）

4．先化简，再求值：$\frac{b}{{a}^{2}-{b}^{2}}$÷（$1-\frac{a}{a+b}$），其中a=2016，b=2015．

5．一组数据3、4、x、1、4、3有唯一的众数3，则这组数据的中位数是（　　）

试题分类