题目内容
5. 如图,已知直线y=kx+b与双曲线y=$\frac{m}{x}$(x<0)交于A(x1,y1),B(x2,y2),且x1≠x2,直线AB交x轴于点C(x0,0).
如图,已知直线y=kx+b与双曲线y=$\frac{m}{x}$(x<0)交于A(x1,y1),B(x2,y2),且x1≠x2,直线AB交x轴于点C(x0,0).(1)若A(-1,4),B(-2,y2),求直线AB的解析式及C点的坐标;
(2)若C(-4,0),B(-3,1),求A点的坐标;
(3)设点M($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$)为线段AB的中点,记$\frac{{x}_{1}+{x}_{2}}{2}$=t,直接写出t与x0之间的关系为x0=2t.(不要求证明)
分析 (1)将点A(-1,4)代入y=$\frac{m}{x}$,求出反比例函数解析式,将B(-2,y2)代入,求出y2的值,再将A、B两点坐标代入y=kx+b,利用待定系数法求出直线AB的解析式,进而求出C点的坐标;
(2)把C(-4,0),B(-3,1)代入y=kx+b,利用待定系数法求出直线AB的解析式,把B(-3,1)代入y=$\frac{m}{x}$,求出双曲线的解析式,将直线与双曲线的解析式联立组成方程组,解方程组即可求出A点的坐标;
(3)将点A(x1,y1),B(x2,y2)代入y=kx+b,利用待定系数法求出直线AB的解析式,再求出C点的坐标,由双曲线y=$\frac{m}{x}$(x<0)过点A(x1,y1),B(x2,y2),得出x1•y1=x2•y2=m,那么x0=x1+x2,进而得出x0=2t.
解答 解:(1)∵双曲线y=$\frac{m}{x}$(x<0)过点A(-1,4),B(-2,y2),
∴m=-1×4=-4,-2y2=m,
∴y=-$\frac{4}{x}$,y2=2,
∵直线y=kx+b过点A(-1,4),B(-2,2),
∴$\left\{\begin{array}{l}{-k+b=4}\\{-2k+b=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=2}\\{b=6}\end{array}\right.$,
∴直线AB的解析式为y=2x+6,
当y=0时,2x+6=0,解得x=-3,
∴C点的坐标为(-3,0);
(2)∵直线y=kx+b过点C(-4,0),B(-3,1),
∴$\left\{\begin{array}{l}{-4k+b=0}\\{-3k+b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=4}\end{array}\right.$,
∴直线AB的解析式为y=x+4.
∵双曲线y=$\frac{m}{x}$(x<0)过点B(-3,1),
∴m=-3×1=-3,
∴y=-$\frac{3}{x}$,
由$\left\{\begin{array}{l}{y=x+4}\\{y=-\frac{3}{x}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$,或$\left\{\begin{array}{l}{x=-3}\\{y=1}\end{array}\right.$,
∴A点的坐标为(-1,3);
(3)∵直线y=kx+b过点A(x1,y1),B(x2,y2),
∴$\left\{\begin{array}{l}{k{x}_{1}+b={y}_{1}}\\{k{x}_{2}+b={y}_{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}}\\{b=\frac{{x}_{2}{y}_{1}-{x}_{1}{y}_{2}}{{x}_{2}-{x}_{1}}}\end{array}\right.$,
∴y=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$x+$\frac{{x}_{2}{y}_{1}-{x}_{1}{y}_{2}}{{x}_{2}-{x}_{1}}$,
当y=0时,$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$x+$\frac{{x}_{2}{y}_{1}-{x}_{1}{y}_{2}}{{x}_{2}-{x}_{1}}$=0,解得x=$\frac{{x}_{1}{y}_{2}-{x}_{2}{y}_{1}}{{y}_{2}-{y}_{1}}$,
∴C点的坐标为($\frac{{x}_{1}{y}_{2}-{x}_{2}{y}_{1}}{{y}_{2}-{y}_{1}}$,0);
∵双曲线y=$\frac{m}{x}$(x<0)过点A(x1,y1),B(x2,y2),
∴x1•y1=x2•y2=m,
∴y1=$\frac{m}{{x}_{1}}$,y2=$\frac{m}{{x}_{2}}$,
∴x0=$\frac{{x}_{1}{y}_{2}-{x}_{2}{y}_{1}}{{y}_{2}-{y}_{1}}$=$\frac{{x}_{1}•\frac{m}{{x}_{2}}-{x}_{2}•\frac{m}{{x}_{1}}}{\frac{m}{{x}_{2}}-\frac{m}{{x}_{1}}}$=$\frac{{mx}_{1}^{2}-{mx}_{2}^{2}}{m{x}_{1}-m{x}_{2}}$=x1+x2,
∵$\frac{{x}_{1}+{x}_{2}}{2}$=t,
∴x0=2t.
故答案为x0=2t.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了利用待定系数法求直线与双曲线的解析式.

 口算题天天练系列答案
口算题天天练系列答案| A. | -a4a3=a7 | B. | (-a)4a3=a12 | C. | (a4)3=a12 | D. | a4+a3=a7 |
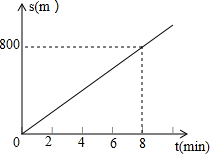 小灰灰和灰太狼一起进行晨练,小灰灰从狼堡先跑8分钟后,灰太狼才从同一起点沿同一路线开始跑,它们的速度一直保持不变,经过2分钟后两人相遇,小灰灰跑过的路程s和所用的时间t之间的关系如图所示,根据图象回答下列问题:
小灰灰和灰太狼一起进行晨练,小灰灰从狼堡先跑8分钟后,灰太狼才从同一起点沿同一路线开始跑,它们的速度一直保持不变,经过2分钟后两人相遇,小灰灰跑过的路程s和所用的时间t之间的关系如图所示,根据图象回答下列问题:



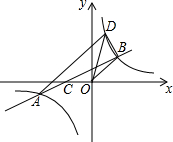 如图,点A和点B分别是反比例函数y=$\frac{k}{x}$(k≠0)图象上两点,连接AB交x轴负半轴于点C,连接BO,tan∠BCO=$\frac{1}{2}$,∠BOC=135°,CO=2,过点A作AD∥BO交反比例函数y=$\frac{k}{x}$于点D,连接OD,BD.
如图,点A和点B分别是反比例函数y=$\frac{k}{x}$(k≠0)图象上两点,连接AB交x轴负半轴于点C,连接BO,tan∠BCO=$\frac{1}{2}$,∠BOC=135°,CO=2,过点A作AD∥BO交反比例函数y=$\frac{k}{x}$于点D,连接OD,BD.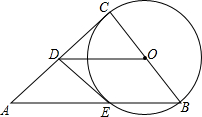 在△ABC中,∠ACB=90°,以BC为直径作圆O,交斜边AB于E,D是AC的中点,连接DE.
在△ABC中,∠ACB=90°,以BC为直径作圆O,交斜边AB于E,D是AC的中点,连接DE. 如图,已知点A(1,2)是函数y=$\frac{2}{x}$(x>0)的图象上的点,连接0A作0A⊥0B,与图象y=$\frac{-6}{x}$(x>0)交于点B.
如图,已知点A(1,2)是函数y=$\frac{2}{x}$(x>0)的图象上的点,连接0A作0A⊥0B,与图象y=$\frac{-6}{x}$(x>0)交于点B. 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,连接EF交AP于点G.给出以下四个结论:①∠B=∠C=45°;②AE=CF;③△EPF是等腰直角三角形;④四边形AEPF的面积是△ABC面积的一半.其中正确的有( )
如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,连接EF交AP于点G.给出以下四个结论:①∠B=∠C=45°;②AE=CF;③△EPF是等腰直角三角形;④四边形AEPF的面积是△ABC面积的一半.其中正确的有( )