题目内容
9. 如图,矩形ABCD的对角线AC,BD的和是20,且BC=2AB,则AB的长度为2$\sqrt{5}$.
如图,矩形ABCD的对角线AC,BD的和是20,且BC=2AB,则AB的长度为2$\sqrt{5}$.
分析 由矩形的性质和勾股定理得出AB2+4AB2=102,即可得出结果.
解答 解:∵四边形ABCD是矩形,
∴∠ABC=90°,AC=BD,
∵AC+BD=20,
∴AC=BD=10,
由勾股定理得:AB2+BC2=AC2,
∵BC=2AB,
∴AB2+4AB2=102,
解得:AB=2$\sqrt{5}$;
故答案为:2$\sqrt{5}$.
点评 本题考查了矩形的性质、勾股定理;熟练掌握矩形的性质,由勾股定理得出方程是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列运算正确的是( )
| A. | -a4a3=a7 | B. | (-a)4a3=a12 | C. | (a4)3=a12 | D. | a4+a3=a7 |
1. 如图,点B、E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是( )
如图,点B、E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是( )
 如图,点B、E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是( )
如图,点B、E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是( )| A. | BC=FD,AC=ED | B. | ∠A=∠DEF,AC=ED | C. | AC=ED,AB=EF | D. | ∠ABC=∠EFD,BC=FD |
18.已知反比例函数y=$\frac{1}{x}$,下列结论中不正确的是( )
| A. | 图象经过点(-$\frac{1}{2}$,-2) | B. | 图象位于第一、三象限 | ||
| C. | y随x的增大而减小 | D. | 当1<x<3时,y的取值范围是$\frac{1}{3}$<y<1 |
 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,连接EF交AP于点G.给出以下四个结论:①∠B=∠C=45°;②AE=CF;③△EPF是等腰直角三角形;④四边形AEPF的面积是△ABC面积的一半.其中正确的有( )
如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,连接EF交AP于点G.给出以下四个结论:①∠B=∠C=45°;②AE=CF;③△EPF是等腰直角三角形;④四边形AEPF的面积是△ABC面积的一半.其中正确的有( )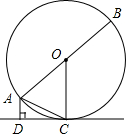 如图,AB分别是⊙O的直径,AC是弦,DC是⊙O的切线,C为切点,AD⊥DC于点D.
如图,AB分别是⊙O的直径,AC是弦,DC是⊙O的切线,C为切点,AD⊥DC于点D.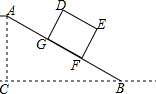 如图,水平面上有一个坡度i=1:2的斜坡AB,矩形货柜DEFG放置在斜坡上,己知DE=2.5m.EF=2m,BF=3.5m,则点D离地面的高DH为2$\sqrt{5}$m.(结果保留根号)
如图,水平面上有一个坡度i=1:2的斜坡AB,矩形货柜DEFG放置在斜坡上,己知DE=2.5m.EF=2m,BF=3.5m,则点D离地面的高DH为2$\sqrt{5}$m.(结果保留根号)