题目内容
19.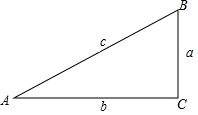 如图,在△ABC中,∠C=90°,定义:斜边与∠A的邻边的比叫做∠A的正割,用“secA”表示,如设该直角三角形各边为a,b,c,则secA=$\frac{c}{b}$,则下列说法正确的是( )
如图,在△ABC中,∠C=90°,定义:斜边与∠A的邻边的比叫做∠A的正割,用“secA”表示,如设该直角三角形各边为a,b,c,则secA=$\frac{c}{b}$,则下列说法正确的是( )| A. | secB•sinA=1 | B. | secB=$\frac{b}{c}$ | C. | secA•cosB=1 | D. | sec2A•sec2B=1 |
分析 根据正割的定义:斜边与∠A的邻边的比进行计算,再选择即可.
解答 解:∵secA=$\frac{c}{b}$,
∴secB=$\frac{c}{a}$,
∴secB•sinA=$\frac{c}{a}$•$\frac{a}{c}$=1,故A错误;
∴secB=$\frac{c}{a}$,故B错误;
∴secA•cosB=$\frac{c}{b}$•$\frac{a}{c}$=$\frac{a}{b}$,故C错误;
∴sec2A•sec2B=$\frac{{c}^{2}}{{b}^{2}}$•$\frac{{c}^{2}}{{a}^{2}}$=$\frac{{c}^{4}}{{a}^{2}{b}^{2}}$,故D错误;
故选A.
点评 本题考查了锐角三角函数的定义,掌握正割的定义:斜边与∠A的邻边的比叫做∠A的正割,用“secA”表示,是解题的关键.

练习册系列答案
相关题目
10. 如图是小明作线段AB的垂直平分线的作法及作图痕迹,则四边形ADBC一定是( )
如图是小明作线段AB的垂直平分线的作法及作图痕迹,则四边形ADBC一定是( )
 如图是小明作线段AB的垂直平分线的作法及作图痕迹,则四边形ADBC一定是( )
如图是小明作线段AB的垂直平分线的作法及作图痕迹,则四边形ADBC一定是( )| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 无法确定 |
6. 如图,一个螺母的实物图,它的俯视图应该是( )
如图,一个螺母的实物图,它的俯视图应该是( )
 如图,一个螺母的实物图,它的俯视图应该是( )
如图,一个螺母的实物图,它的俯视图应该是( )| A. |  | B. |  | C. |  | D. |  |
 如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F.
如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F.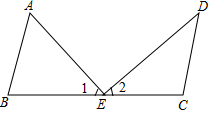 如图,已知AB∥CD,E是BC上一点,∠1=∠A,∠2=∠D,求证:AE⊥DE.
如图,已知AB∥CD,E是BC上一点,∠1=∠A,∠2=∠D,求证:AE⊥DE.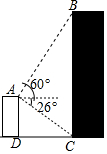 如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯楼的高度,测得电梯楼顶部B处的仰角为60°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.73,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯楼的高度,测得电梯楼顶部B处的仰角为60°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.73,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)