题目内容
4.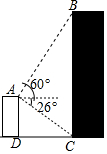 如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯楼的高度,测得电梯楼顶部B处的仰角为60°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.73,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯楼的高度,测得电梯楼顶部B处的仰角为60°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.73,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
分析 首先过点A作AE⊥BC于E,可得四边形ADCE是矩形,即可得CE=AD=15米,然后分别在Rt△ACE中,AE=$\frac{CE}{tan26°}$与在Rt△ABE中,BE=AE•tan60°,即可求得BE的长,继而求得电梯楼的高度.
解答 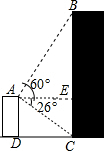 解:过点A作AE⊥BC于E,
解:过点A作AE⊥BC于E,
∵AD⊥CD,BC⊥CD,
∴四边形ADCE是矩形,
∴CE=AD=15米,
在Rt△ACE中,AE=$\frac{CE}{tan26°}$=$\frac{15}{0.49}$≈30.6(米),
在Rt△ABE中,BE=AE•tan60°=52.9(米),
∴BC=CE+BE=15+52.9=67.9(米).
答:电梯楼的高度BC为67.9米.
点评 此题考查了仰角与俯角的知识.此题难度适中,注意能借助仰角或俯角构造直角三角形并解直角三角形是解此题的关键.

练习册系列答案
相关题目
19.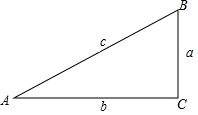 如图,在△ABC中,∠C=90°,定义:斜边与∠A的邻边的比叫做∠A的正割,用“secA”表示,如设该直角三角形各边为a,b,c,则secA=$\frac{c}{b}$,则下列说法正确的是( )
如图,在△ABC中,∠C=90°,定义:斜边与∠A的邻边的比叫做∠A的正割,用“secA”表示,如设该直角三角形各边为a,b,c,则secA=$\frac{c}{b}$,则下列说法正确的是( )
 如图,在△ABC中,∠C=90°,定义:斜边与∠A的邻边的比叫做∠A的正割,用“secA”表示,如设该直角三角形各边为a,b,c,则secA=$\frac{c}{b}$,则下列说法正确的是( )
如图,在△ABC中,∠C=90°,定义:斜边与∠A的邻边的比叫做∠A的正割,用“secA”表示,如设该直角三角形各边为a,b,c,则secA=$\frac{c}{b}$,则下列说法正确的是( )| A. | secB•sinA=1 | B. | secB=$\frac{b}{c}$ | C. | secA•cosB=1 | D. | sec2A•sec2B=1 |
11.下列由等式的性质进行的变形,错误的是( )
| A. | 如果a=b,那么a-5=b-5 | B. | 如果a=b,那么-$\frac{a}{2}$=-$\frac{b}{2}$ | ||
| C. | 如果a=3,那么a2=3a | D. | 如果$\frac{c}{a}=\frac{c}{b}$,那么a=b |