题目内容
7．若常数k使多项式y2-3（k+1）y+9是一个完全平方式，则k=1或-3．分析 先根据两平方项项确定出这两个数是x和3，再根据完全平方公式求解即可．
解答 解：∵y2-3（k+1）y+9=y2-3（k+1）y+32，
∴-3（k+1）y=±2×y×3，
∴k+1=±2，
解得k=1或-3．
故答案为1或-3．
点评 本题是完全平方公式的应用，两数的平方和，再加上或减去它们积的2倍，就构成了一个完全平方式．此题解题的关键是利用平方项来确定这两个数．
练习册系列答案
名题金卷系列答案
相关题目
19．
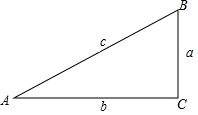如图，在△ABC中，∠C=90°，定义：斜边与∠A的邻边的比叫做∠A的正割，用“secA”表示，如设该直角三角形各边为a，b，c，则secA=$\frac{c}{b}$，则下列说法正确的是（ ）
如图，在△ABC中，∠C=90°，定义：斜边与∠A的邻边的比叫做∠A的正割，用“secA”表示，如设该直角三角形各边为a，b，c，则secA=$\frac{c}{b}$，则下列说法正确的是（ ）| A． | secB•sinA=1 | B． | secB=$\frac{b}{c}$ | C． | secA•cosB=1 | D． | sec2A•sec2B=1 |
18．下列运算中，计算正确的是（ ）
| A． | 3x2+2x2=5x 4 | B． | （-x2）3=-x 6 | C． | （2x2y）2=2x4y2 | D． | （x+y2）2=x2+y4 |
如图所示，根据几何体的三视图及其尺寸解答下列问题