题目内容
20.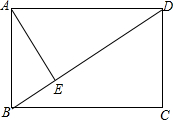 如图所示,在矩形ABCD中,AD的长为8cm,对角线BD比AB边长4cm.
如图所示,在矩形ABCD中,AD的长为8cm,对角线BD比AB边长4cm.(1)求AB的长;
(2)求点A到BD的距离AE的长.
分析 (1)设AB为xcm,则BD为(x+4)cm;由四边形ABCD是矩形,得出∠BAD=90°,由勾股定理得出AB2+AD2=BD2,即x2+82=(x+4)2,解方程即可求出AB的长;
(2)由BD=6cm+4cm=10cm,△ABD的面积=$\frac{1}{2}$×10×AE=$\frac{1}{2}$×8×6,即可求出AE.
解答 解:(1)设AB为xcm,则BD为(x+4)cm;
∵四边形ABCD是矩形,
∴∠BAD=90°,BC=AD=8cm,CD=AB,
∴AB2+AD2=BD2,
即x2+82=(x+4)2,
解得:x=6,
即AB的长为6cm;
(2)∵BD=6cm+4cm=10cm,
又∵△ABD的面积=$\frac{1}{2}$×10×AE=$\frac{1}{2}$×8×6,
∴AE=4.8(cm).
点评 本题考查了矩形的性质、勾股定理以及三角形面积的计算;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
5.若y-1与2-x成正比例,则下列说法正确的是( )
| A. | y是x的一次函数 | B. | y是x的正比例函数 | ||
| C. | y是x的函数但不是正比例函数 | D. | y不是x的函数 |
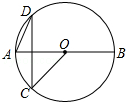 如图,AB是⊙O的直径,C,D是⊙O上两点,CD⊥AB.若∠DAB=65°,则∠AOC=50°.
如图,AB是⊙O的直径,C,D是⊙O上两点,CD⊥AB.若∠DAB=65°,则∠AOC=50°.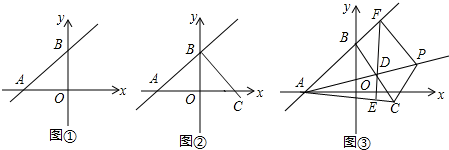
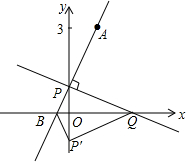 如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(1,3),点P的坐标是(0,b)(b≠0).直线AP交x轴于点B,记点P关于x轴的对称点为P′,点Q为x轴上一动点.
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(1,3),点P的坐标是(0,b)(b≠0).直线AP交x轴于点B,记点P关于x轴的对称点为P′,点Q为x轴上一动点.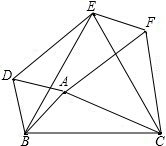 如图,分别以△ABC的三边为边长,在BC的同侧作等边△ABD,等边△BCE,等边△ACF,连接DE,EF.求证:四边形ADEF是平行四边形.
如图,分别以△ABC的三边为边长,在BC的同侧作等边△ABD,等边△BCE,等边△ACF,连接DE,EF.求证:四边形ADEF是平行四边形.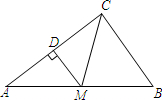 如图,在△ABC中,点M在边AB上,AM=CM,DM⊥AC,且DM∥BC,说明△CMB是等腰三角形.
如图,在△ABC中,点M在边AB上,AM=CM,DM⊥AC,且DM∥BC,说明△CMB是等腰三角形.