题目内容
12.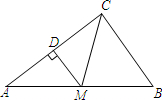 如图,在△ABC中,点M在边AB上,AM=CM,DM⊥AC,且DM∥BC,说明△CMB是等腰三角形.
如图,在△ABC中,点M在边AB上,AM=CM,DM⊥AC,且DM∥BC,说明△CMB是等腰三角形.
分析 根据已知条件,证出∠A=∠MCD,再根据平行线的性质,证出∠B=∠MCB,最后根据等角对等边得出MC=MB,即可得出△CMB是等腰三角形.
解答 解:在△AMC中,
∵AM=CM,DM⊥AC,
∴∠A=∠MCD,
∴∠AMD=∠DMC,
∵DM∥BC (已知),
∴∠DMC=∠MCB (两直线平行,内错角相等),
∠AMD=∠B (两直线平行,同位角相等),
∴∠B=∠MCB (等量代换),
∴MC=MB (等角对等边),
∴△CMB是等腰三角形.
点评 本题考查了等腰三角形的判定及性质,掌握角的等量代换和平行线的性质是本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.已知一元一次方程k1x+b1=0的解为x=-2,一元一次方程k2x+b2=0的解为x=3,则直线y=k1x+b1与x轴的交点A到直线y=k2x+b2与x轴的交点B之间的距离为( )
| A. | 1 | B. | 5 | C. | 6 | D. | 无法确定 |
9.已知三角形的两边长分别为5和8,则三角形的第三边不可能是( )
| A. | 4 | B. | 6 | C. | 8 | D. | 13 |
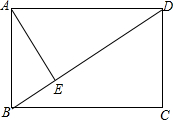 如图所示,在矩形ABCD中,AD的长为8cm,对角线BD比AB边长4cm.
如图所示,在矩形ABCD中,AD的长为8cm,对角线BD比AB边长4cm.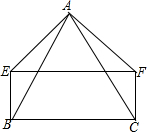 如图,AB=AC,AE=AF,且∠EAB=∠FAC,EF=BC,求证:四边形EBCF是矩形.
如图,AB=AC,AE=AF,且∠EAB=∠FAC,EF=BC,求证:四边形EBCF是矩形.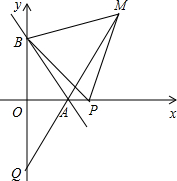 如图,直线AB交x轴正半轴于点A(a,0),交y轴正半轴于点B(0,b),且a、b满足(a-b)2+$\sqrt{{b}^{2}-16}$=0
如图,直线AB交x轴正半轴于点A(a,0),交y轴正半轴于点B(0,b),且a、b满足(a-b)2+$\sqrt{{b}^{2}-16}$=0