题目内容
15.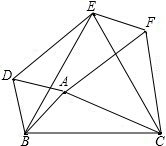 如图,分别以△ABC的三边为边长,在BC的同侧作等边△ABD,等边△BCE,等边△ACF,连接DE,EF.求证:四边形ADEF是平行四边形.
如图,分别以△ABC的三边为边长,在BC的同侧作等边△ABD,等边△BCE,等边△ACF,连接DE,EF.求证:四边形ADEF是平行四边形.
分析 根据等边三角形的性质推出∠BCE=∠FCA=60°,求出∠BCA=∠FCE,证△BCA≌△ECF,推出AD=EF=AB,同理得出DE=AF,即可得出结论.
解答  证明:∵△BCE、△ACF、△ABD都是等边三角形,
证明:∵△BCE、△ACF、△ABD都是等边三角形,
∴AB=AD,AC=CF,BC=CE,∠BCE=∠ACF,
∴∠BCE-∠ACE=∠ACF-∠ACE,
即∠BCA=∠FCE,
在△BCA和△ECF中,
$\left\{\begin{array}{l}{BC=CE}\\{∠BCA=∠ECF}\\{AC=CF}\end{array}\right.$,
∴△BCA≌△ECF(SAS),
∴AB=EF,
∵AB=AD,
∴AD=EF,
同理:△BDE≌△BAC,
∴DE=AF,
∴四边形ADEF是平行四边形.
点评 此题主要考查了等边三角形的性质和平行四边形的判定以及全等三角形的判定与性质,得出△BCA≌△ECF是解题关键.

练习册系列答案
相关题目
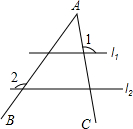
5. 如图,将三角板的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )
如图,将三角板的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )
 如图,将三角板的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )
如图,将三角板的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )| A. | 10° | B. | 15° | C. | 25° | D. | 35° |
6. 如图,∠A被平行直线l1、l2所截,若∠1=100°,∠2=125°,则∠A的度数是( )
如图,∠A被平行直线l1、l2所截,若∠1=100°,∠2=125°,则∠A的度数是( )
 如图,∠A被平行直线l1、l2所截,若∠1=100°,∠2=125°,则∠A的度数是( )
如图,∠A被平行直线l1、l2所截,若∠1=100°,∠2=125°,则∠A的度数是( )| A. | 25° | B. | 30° | C. | 35° | D. | 45° |
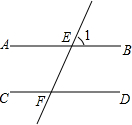 已知,直线AB、CD被EF所截,∠AEF=∠EFD,求证:AB∥CD.
已知,直线AB、CD被EF所截,∠AEF=∠EFD,求证:AB∥CD.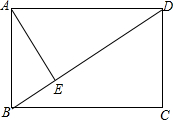 如图所示,在矩形ABCD中,AD的长为8cm,对角线BD比AB边长4cm.
如图所示,在矩形ABCD中,AD的长为8cm,对角线BD比AB边长4cm.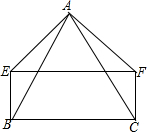 如图,AB=AC,AE=AF,且∠EAB=∠FAC,EF=BC,求证:四边形EBCF是矩形.
如图,AB=AC,AE=AF,且∠EAB=∠FAC,EF=BC,求证:四边形EBCF是矩形.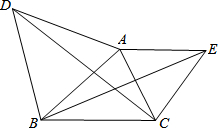 如图,△ABD、△AEC都是等边三角形.
如图,△ABD、△AEC都是等边三角形.