题目内容
9.如图①,用直尺和圆规作一个角等于已知角,过程中先利用SSS判定三角形全等,从而说明∠A′O′B′=∠AOB如图②,作一个角的平分线,过程先利用SSS判定三角形全等,从而说明OP平分∠AOB(填“SSS”“SAS”“ASA”或“AAS”)
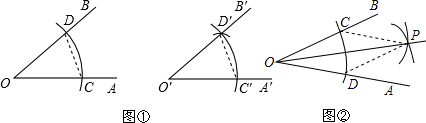
分析 ①连接CD、C′D′,从作图可知OD=OD′=OC=OC′,CD=C′D′,根据SSS证△ODC≌△O′D′C′,根据全等三角形的对应角相等推出即可;
②由作图可得CO=DO,CP=DP,OP=OP,可利用SSS定理判定三角形全等,根据全等三角形的对应角相等推出即可.
解答 解:①连接CD、C′D′,
从作图可知OD=OD′=OC=OC′,CD=C′D′,
在△ODC和△O′D′C′中
$\left\{\begin{array}{l}{OD=OD′}\\{OC=OC′}\\{CD=C′D′}\end{array}\right.$,
∴△ODC≌△O′D′C′(SSS),
∴∠A′O′B′=∠AOB(全等三角形的对应角相等);
②在△OCP和△ODP中,
$\left\{\begin{array}{l}{CO=DO}\\{CP=DP}\\{OP=OP}\end{array}\right.$,
∴△OCP≌△ODP(SSS),
∴∠COP=∠DOP(全等三角形的对应角相等).
故答案为:SSS,SSS.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.也考查了作图-基本作图.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
19. 某教研部门为了了解在校初中生阅读教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某教研部门为了了解在校初中生阅读教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某校初中生阅读教科书情况统计图表
(1)求样本容量及表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2500名,请估计该校“重视阅读教科书”的初中人数;
(3)①根据上面的统计结果,谈谈你对该校初中生阅读教科书的现状的看法及建议;
②如果要了解全省初中生阅读教科书的情况,你认为应该如何进行抽样?
 某教研部门为了了解在校初中生阅读教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某教研部门为了了解在校初中生阅读教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:某校初中生阅读教科书情况统计图表
| 类别 | 人数 | 占总人数比例 |
| 重视 | a | b |
| 一般 | 57 | 0.285 |
| 不重视 | c | 0.36 |
| 说不清楚 | 9 | 0.045 |
(2)若该校共有初中生2500名,请估计该校“重视阅读教科书”的初中人数;
(3)①根据上面的统计结果,谈谈你对该校初中生阅读教科书的现状的看法及建议;
②如果要了解全省初中生阅读教科书的情况,你认为应该如何进行抽样?
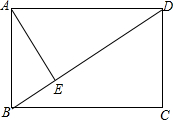 如图所示,在矩形ABCD中,AD的长为8cm,对角线BD比AB边长4cm.
如图所示,在矩形ABCD中,AD的长为8cm,对角线BD比AB边长4cm.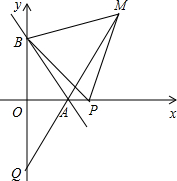 如图,直线AB交x轴正半轴于点A(a,0),交y轴正半轴于点B(0,b),且a、b满足(a-b)2+$\sqrt{{b}^{2}-16}$=0
如图,直线AB交x轴正半轴于点A(a,0),交y轴正半轴于点B(0,b),且a、b满足(a-b)2+$\sqrt{{b}^{2}-16}$=0