题目内容
20.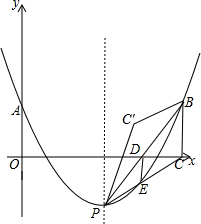 如图,抛物线y=a(x-$\sqrt{2}$m)2-m(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m).点A关于直线l的对称点为B,作BC⊥x轴于点C,连接PC、PB,与抛物线、x轴分别相交于点D、E,连接DE.将△PBC沿直线PB翻折,得到△PBC′.
如图,抛物线y=a(x-$\sqrt{2}$m)2-m(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m).点A关于直线l的对称点为B,作BC⊥x轴于点C,连接PC、PB,与抛物线、x轴分别相交于点D、E,连接DE.将△PBC沿直线PB翻折,得到△PBC′.(1)该抛物线的解析式为y=$\frac{1}{m}(x-\sqrt{2}m)^{2}-m$;(用含m的式子表示);
(2)探究线段DE、BC的关系,并证明你的结论;
(3)直接写出C′点的坐标(用含m的式子表示).
分析 (1)将点A的坐标代入抛物线解析式,即可求出a的值;
(2)根据抛物线的解析式,求出顶点P的坐标,根据对称轴,求出点B,C的坐标,根据待定系数法求出直线BP、CP的解析式,求出点D、E的坐标,进而求出DE,BC的长度,即可解得;
(3)连接CC′交直线BP于点F,则CC′⊥BP,且CF=C′F,求出CC′的解析式,进而求得点F的坐标,根据CF=C′F,即可解答.
解答 解:(1)把点A(0,m)代入y=$a(x-2\sqrt{2}m)^{2}-m$,
得:2am2-m=m,
am-1=0,
∵am>1,
∴a=$\frac{1}{m}$,
∴y=$\frac{1}{m}(x-\sqrt{2}m)^{2}-m$,
故答案为:y=$\frac{1}{m}(x-\sqrt{2}m)^{2}-m$;
(2)DE=$\frac{1}{2}$BC.
理由:又抛物线y=$\frac{1}{m}(x-\sqrt{2}m)^{2}-m$,可得抛物线的顶点坐标P($\sqrt{2}$m,-m),
由l:x=$\sqrt{2}$m,可得:点B(2$\sqrt{2}$m,m),
∴点C(2$\sqrt{2}$m,0).
设直线BP的解析式为y=kx+b,点P($\sqrt{2}$m,-m)和点B(2$\sqrt{2}$m,m)在这条直线上,
得:$\left\{\begin{array}{l}{\sqrt{2}mk+b=-m}\\{2\sqrt{2}mk+b=m}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\sqrt{2}}\\{b=-3m}\end{array}\right.$,
∴直线BP的解析式为:y=$\sqrt{2}$x-3m,
令y=0,$\sqrt{2}$x-3m=0,解得:x=$\frac{3\sqrt{2}}{2}m$,
∴点D($\frac{3\sqrt{2}}{2}m$,0);
设直线CP的解析式为y=k1x+b1,点P($\sqrt{2}$m,-m)和点C(2$\sqrt{2}$m,0)在这条直线上,
得:$\left\{\begin{array}{l}{2\sqrt{2}m{k}_{1}+{b}_{1}=0}\\{\sqrt{2}m{k}_{1}+{b}_{1}=-m}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{k}_{1}=\frac{\sqrt{2}}{2}}\\{{b}_{1}=-2m}\end{array}\right.$,
∴直线CP的解析式为:y=$\frac{\sqrt{2}}{2}$x-2m;
抛物线与直线CP相交于点E,可得:$\left\{\begin{array}{l}{y=\frac{1}{m}(x-2m)^{2}-m}\\{y=\frac{\sqrt{2}}{2}x-2m}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{x}_{1}=\frac{3\sqrt{2}}{2}m}\\{{y}_{1}=-\frac{m}{2}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\sqrt{2}m}\\{{y}_{2}=-m}\end{array}\right.$(舍去),
∴点E($\frac{3\sqrt{2}}{2}m$,-$\frac{m}{2}$);
∵xD=xE,
∴DE⊥x轴,
∴DE=yD-yE=$\frac{m}{2}$,BC=yB-yC=m=2DE,
即DE=$\frac{1}{2}$BC;
(3)C′($\frac{4\sqrt{2}}{3}m$,$\frac{2}{3}m$).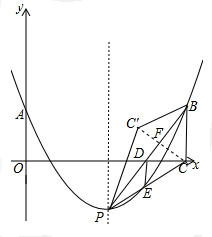
连接CC′,交直线BP于点F,
∵BC′=BC,∠C′BF=∠CBF,
∴CC′⊥BP,CF=C′F,
设直线BP的解析式为y=kx+b,点B(2$\sqrt{2}$m,m),P($\sqrt{2}$m,-m)在直线上,
∴$\left\{\begin{array}{l}{2\sqrt{2}mk+b=m}\\{\sqrt{2}mk+b=-m}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\sqrt{2}}\\{b=-3m}\end{array}\right.$,
∴直线BP的解析式为:y=$\sqrt{2}$x-3m,
∵CC′⊥BP,
∴设直线CC′的解析式为:y=$-\frac{\sqrt{2}}{2}$x+b1,
∴$-\frac{\sqrt{2}}{2}×2\sqrt{2}m+{b}_{1}=0$,解得:b1=2m,
联立①②,得:$\left\{\begin{array}{l}{y=\sqrt{2}x-3m}\\{y=-\frac{\sqrt{2}}{2}x+2m}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=\frac{5\sqrt{2}}{3}m}\\{y=\frac{m}{3}}\end{array}\right.$,
∴点F($\frac{5\sqrt{2}}{3}m$,$\frac{m}{3}$),
∴CF=$\sqrt{(\frac{5\sqrt{2}}{3}m-2\sqrt{2}m)^{2}+(\frac{m}{3})^{2}}$=$\frac{\sqrt{3}}{3}m$,
设点C′的坐标为(a,$-\frac{\sqrt{2}}{2}a+2m$),
∴C′F=$\sqrt{(\frac{5\sqrt{2}}{3}m-a)^{2}+(\frac{m}{3}+\frac{\sqrt{2}}{2}a-2m)^{2}}$=$\frac{\sqrt{3}}{3}m$,解得:a=$\frac{4\sqrt{2}}{3}m$,
∴$-\frac{\sqrt{2}}{2}a+2m=\frac{2}{3}m$,
∴C′($\frac{4\sqrt{2}}{3}m$,$\frac{2}{3}m$).
点评 本题主要考查二次函数与一次函数的综合运用,能够熟练求出直线的解析式和各点的坐标是解决此题的关键.

 口算题天天练系列答案
口算题天天练系列答案| A. | m<3 | B. | m≤3 | C. | m<3且m≠2 | D. | m≤3且m≠2 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,矩形纸片ABCD,AB=2,点E在BC上,且AE=EC,若将纸片沿AE折叠,使点B落在AC上,求AE的长.
如图,矩形纸片ABCD,AB=2,点E在BC上,且AE=EC,若将纸片沿AE折叠,使点B落在AC上,求AE的长.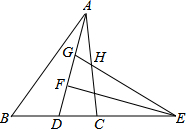 如图,在△ABC中,5AB=6AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则$\frac{AG}{FD}$的值为$\frac{10}{7}$.
如图,在△ABC中,5AB=6AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则$\frac{AG}{FD}$的值为$\frac{10}{7}$.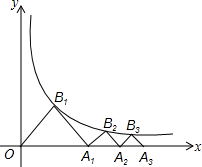 已知反比例函数$y=\frac{4}{x}$,作等腰Rt△OA1B1,使点B1在反例函数的图象上,点A1在x轴上,再作等腰Rt△A1B2A2,使点B2在反比例函数的图象上,点A2在x轴上;…,再作等腰Rt△A8B9A9,则OA9=12.
已知反比例函数$y=\frac{4}{x}$,作等腰Rt△OA1B1,使点B1在反例函数的图象上,点A1在x轴上,再作等腰Rt△A1B2A2,使点B2在反比例函数的图象上,点A2在x轴上;…,再作等腰Rt△A8B9A9,则OA9=12.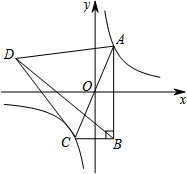 如图,已知双曲线y=$\frac{k}{x}$(k≠0)与正比例函数y=mx(m≠0)交于A、C两点,以AC为边作等边三角形ACD,且S△ACD=20$\sqrt{3}$,再以AC为斜边作直角三角形ABC,使AB∥y轴,连接BD.若△ABD的周长比△BCD的周长多4,则k=( )
如图,已知双曲线y=$\frac{k}{x}$(k≠0)与正比例函数y=mx(m≠0)交于A、C两点,以AC为边作等边三角形ACD,且S△ACD=20$\sqrt{3}$,再以AC为斜边作直角三角形ABC,使AB∥y轴,连接BD.若△ABD的周长比△BCD的周长多4,则k=( )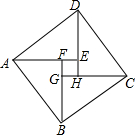 如图,由四个全等的直角三角形拼成“赵爽弦图”. Rt△ABF中,∠AFB=90°,AF=3,AB=5.四边形EFGH的面积是1.
如图,由四个全等的直角三角形拼成“赵爽弦图”. Rt△ABF中,∠AFB=90°,AF=3,AB=5.四边形EFGH的面积是1.