题目内容
8.若关于x的一元二次方程(m-2)x2-2x+1=0有实根,则m的取值范围是( )| A. | m<3 | B. | m≤3 | C. | m<3且m≠2 | D. | m≤3且m≠2 |
分析 由于x的一元二次方程(m-2)x2-2x+1=0有实根,那么二次项系数不等于0,并且其判别式△是非负数,由此可以建立关于m的不等式组,解不等式组即可求出m的取值范围.
解答 解:∵关于x的一元二次方程(m-2)x2-2x+1=0有实根,
∴m-2≠0,并且△=(-2)2-4(m-2)=12-4m≥0,
∴m≤3且m≠2.
故选D.
点评 本题考查了根的判别式的知识,总结:一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
此题切记不要忽略一元二次方程二次项系数不为零这一隐含条件.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
19. 如图,DC是以AB为直径的半圆上的弦,DM⊥CD交AB于点M,CN⊥CD交AB于点N.AB=10,CD=6.则四边形DMNC的面积( )
如图,DC是以AB为直径的半圆上的弦,DM⊥CD交AB于点M,CN⊥CD交AB于点N.AB=10,CD=6.则四边形DMNC的面积( )
 如图,DC是以AB为直径的半圆上的弦,DM⊥CD交AB于点M,CN⊥CD交AB于点N.AB=10,CD=6.则四边形DMNC的面积( )
如图,DC是以AB为直径的半圆上的弦,DM⊥CD交AB于点M,CN⊥CD交AB于点N.AB=10,CD=6.则四边形DMNC的面积( )| A. | 等于24 | B. | 最小为24 | C. | 等于48 | D. | 最大为48 |
17.已知方程①2x+y=0;②$\frac{1}{2}$x+y=2;③x2-x+1=0;④2x+y-3z=7是二元一次方程的是( )
| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ① |
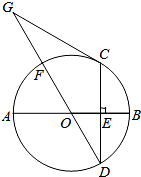 如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°
如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30° 如图,点A在射线OX上,OA的长等于2cm.如果OA绕点O按逆时针方向旋转30°到OA′,那么点A′的位置可以用(2,30°)表示.如果将OA′再沿逆时针方向继续旋转55°到OA′,那么点A′的位置可以用(2,85°)表示.
如图,点A在射线OX上,OA的长等于2cm.如果OA绕点O按逆时针方向旋转30°到OA′,那么点A′的位置可以用(2,30°)表示.如果将OA′再沿逆时针方向继续旋转55°到OA′,那么点A′的位置可以用(2,85°)表示.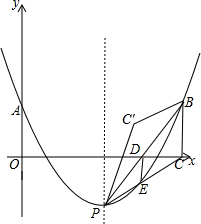 如图,抛物线y=a(x-$\sqrt{2}$m)2-m(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m).点A关于直线l的对称点为B,作BC⊥x轴于点C,连接PC、PB,与抛物线、x轴分别相交于点D、E,连接DE.将△PBC沿直线PB翻折,得到△PBC′.
如图,抛物线y=a(x-$\sqrt{2}$m)2-m(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m).点A关于直线l的对称点为B,作BC⊥x轴于点C,连接PC、PB,与抛物线、x轴分别相交于点D、E,连接DE.将△PBC沿直线PB翻折,得到△PBC′.