题目内容
5.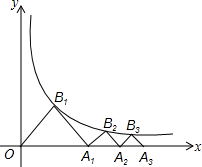 已知反比例函数$y=\frac{4}{x}$,作等腰Rt△OA1B1,使点B1在反例函数的图象上,点A1在x轴上,再作等腰Rt△A1B2A2,使点B2在反比例函数的图象上,点A2在x轴上;…,再作等腰Rt△A8B9A9,则OA9=12.
已知反比例函数$y=\frac{4}{x}$,作等腰Rt△OA1B1,使点B1在反例函数的图象上,点A1在x轴上,再作等腰Rt△A1B2A2,使点B2在反比例函数的图象上,点A2在x轴上;…,再作等腰Rt△A8B9A9,则OA9=12.
分析 先求得OA1=4,然后根据反比例函数图象上点的坐标特征以及等腰直角三角形的性质求得OA2=4$\sqrt{2}$,0A3=4$\sqrt{3}$,…得出规律,即可求得OA9的值.
解答 解:∵反比例函数$y=\frac{4}{x}$,作等腰Rt△OA1B1,
∴B1(2,2),
∴OA1=4,
设Bn的纵坐标为yn,
根据等腰直角三角形的性质:B2(4+y2,y2),
∴y2(y2+4)=4,
解得y2=2$\sqrt{2}$-2,
∴OA2=4+2(2$\sqrt{2}$-2)=4$\sqrt{2}$,
B3(4$\sqrt{2}$+y3,y3),
∴y3(4$\sqrt{2}$+y3)=4,
解得y3=2$\sqrt{3}$-2$\sqrt{2}$,
∴OA3=4$\sqrt{2}$+2(2$\sqrt{3}$-2$\sqrt{2}$)=4$\sqrt{3}$,
B4(4$\sqrt{3}$+y4,y4),
∴y4(4$\sqrt{3}$+y4)=4,
解得y4=4-2$\sqrt{3}$,
∴OA4=4$\sqrt{3}$+2(4-2$\sqrt{3}$)=8=4$\sqrt{4}$,
…
OAn=4$\sqrt{n}$,
∴OA9=4$\sqrt{9}$=12,.
故答案为12.
点评 本题考查了反比例函数图象上点的坐标特征以及等腰直角三角形的性质,表示出Bn的坐标是解题的关键.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
17.已知方程①2x+y=0;②$\frac{1}{2}$x+y=2;③x2-x+1=0;④2x+y-3z=7是二元一次方程的是( )
| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ① |
14.已知a=2013,b=2014,则a2-2ab+b2的值为( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 16216729 |
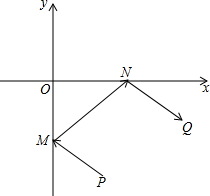 牧马人某天要从马厩牵出马,先到草地边的某一处牧马,再到河边饮水,然后回到帐篷,为了便于研究,以河边为x轴、草地边为y轴建立平面直角坐标系,如图所示,马厩P的坐标为(2,-4),帐篷Q的坐标为(6,-2),请你帮他确定这一天的最短路线.
牧马人某天要从马厩牵出马,先到草地边的某一处牧马,再到河边饮水,然后回到帐篷,为了便于研究,以河边为x轴、草地边为y轴建立平面直角坐标系,如图所示,马厩P的坐标为(2,-4),帐篷Q的坐标为(6,-2),请你帮他确定这一天的最短路线.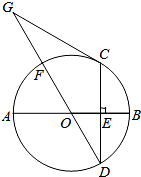 如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°
如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°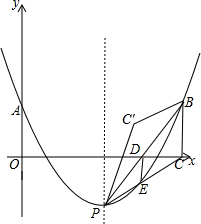 如图,抛物线y=a(x-$\sqrt{2}$m)2-m(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m).点A关于直线l的对称点为B,作BC⊥x轴于点C,连接PC、PB,与抛物线、x轴分别相交于点D、E,连接DE.将△PBC沿直线PB翻折,得到△PBC′.
如图,抛物线y=a(x-$\sqrt{2}$m)2-m(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m).点A关于直线l的对称点为B,作BC⊥x轴于点C,连接PC、PB,与抛物线、x轴分别相交于点D、E,连接DE.将△PBC沿直线PB翻折,得到△PBC′. 如图,方格中有一条美丽可爱的小鱼.
如图,方格中有一条美丽可爱的小鱼.