题目内容
5.若$\frac{a}{ab+a+1}$+$\frac{b}{bc+b+1}$+$\frac{c}{ca+c+1}$=1,则abc=1.分析 设abc=k再设ab+a+1=u,bc+b+1=v,ac+c+1=w根据已知条件,$\frac{a}{u}$+$\frac{b}{v}$+$\frac{c}{w}$=1,通过化简即可得到结果.
解答 解:设abc=k
再设ab+a+1=u,bc+b+1=v,ac+c+1=w
以上三式两边分别乘以c,a,b可得:
abc+ca+c=cu,代入abc=k并根据ac+c+1=w得到:k-1+w=cu①,
abc+ab+a=av,代入abc=k并根据ab+a+1=u得到:k-1+u=av②,
abc+bc+b=bw,代入abc=k并根据bc+b+1=v得到:k-1+v=bw③,
根据已知条件,$\frac{a}{u}$+$\frac{b}{v}$+$\frac{c}{w}$=1,
两边同乘以uvw,得到avw+buw+cuv=uvw,
下面把①式两边乘以v,②式两边乘以w,③式两边乘以u,三式相加得到
(k-1)(u+v+w)+uv+vw+uw=avw+buw+cuv=uvw④
①②③三式相乘,可得:(k-1+u)(k-1+v)(k-1+w)=abcuvw=kuvw,
等号左边把(k-1)看作一项展开,把右边的kuvw移到左边,就有:
(k-1)3+(u+v+w)(k-1)2+(uv+vw+uw)(k-1)-uvw(k-1)=0
(k-1)[(k-1)2+(u+v+w)(k-1)+(uv+vw+uw)-uvw]=0⑤,
把④代入⑤化简为:(k-1)3=0,
所以k=1,
即abc=1.
故答案为:1.
点评 本题考查了分式的加减法,正确的化简是解题的关键.

练习册系列答案
相关题目
4.下列说法中,错误的是( )
| A. | 正多边形的外接圆的圆心,就是它的中心 | |
| B. | 正多边形的外接圆的半径,就是它的半径 | |
| C. | 正多边形的内切圆的半径,就是它的边心距 | |
| D. | 正多边形的外接圆的圆心角,就是它的中心角 |
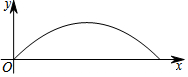 某校足球队在一次训练中,一球员从高2.4米的球门正前方m米处将球射向球门,球射向球门的路线呈抛物线,当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米,建立如图所示的平面直角坐标系
某校足球队在一次训练中,一球员从高2.4米的球门正前方m米处将球射向球门,球射向球门的路线呈抛物线,当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米,建立如图所示的平面直角坐标系
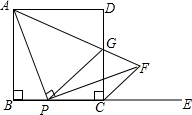 如图,在正方形ABCD中,AB=a,P为边BC上一动点(不与B、C重合),E是边BC延长线上一点,连结AP,过点P作PF⊥AP交∠DCE的平分线于点F,连结AF与边CD交于点G,连结PG.
如图,在正方形ABCD中,AB=a,P为边BC上一动点(不与B、C重合),E是边BC延长线上一点,连结AP,过点P作PF⊥AP交∠DCE的平分线于点F,连结AF与边CD交于点G,连结PG. 如图,△ABC平移得到△DEF,并且DE由线段AB平移而得,AB=BC=4cm,DF=5cm.则△DEF的周长是13cm.
如图,△ABC平移得到△DEF,并且DE由线段AB平移而得,AB=BC=4cm,DF=5cm.则△DEF的周长是13cm.