题目内容
6. 如图,一块矩形绿地ABCD由篱笆围着,并且由一条与AB边平行的篱笆EF分开,已知AB=xm,篱笆的总长为600m.
如图,一块矩形绿地ABCD由篱笆围着,并且由一条与AB边平行的篱笆EF分开,已知AB=xm,篱笆的总长为600m.(1)用含x的代数式表示矩形绿地的面积S;
(2)求矩形绿地的最大面积.
分析 (1)根据题意可以用相应的代数式表示出矩形绿地的面积;
(2)将(1)中的解析式化为顶点式,即可解答本题.
解答 解:(1)由题意可得,
S=x•$\frac{600-3x}{2}$=$-\frac{3}{2}{x}^{2}+300x$,
即S=$-\frac{3}{2}{x}^{2}+300x$;
(2)∵S=$-\frac{3}{2}{x}^{2}+300x$=$-\frac{3}{2}(x-100)^{2}+15000$,
∴当x=100时,S取得最大值,此时,S=15000,
即矩形绿地的最大面积是15000m2.
点评 本题考查二次函数的应用,解答本题的关键是明确题意,列出相应的函数关系式,利用二次函数的顶点式求函数的最值.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
16.若一个多边形从同一个顶点出发可以作4条对角线,则这个多边形的边数为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
14.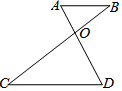 如图,己知$\frac{OA}{DO}$=$\frac{BO}{CO}$=$\frac{1}{2}$,△AOB的面积是100 cm2,则△DOC的面积为( )
如图,己知$\frac{OA}{DO}$=$\frac{BO}{CO}$=$\frac{1}{2}$,△AOB的面积是100 cm2,则△DOC的面积为( )
 如图,己知$\frac{OA}{DO}$=$\frac{BO}{CO}$=$\frac{1}{2}$,△AOB的面积是100 cm2,则△DOC的面积为( )
如图,己知$\frac{OA}{DO}$=$\frac{BO}{CO}$=$\frac{1}{2}$,△AOB的面积是100 cm2,则△DOC的面积为( )| A. | 200 cm2 | B. | 300 cm2 | C. | 400 cm2 | D. | 500 cm2 |
1.已知甲数比乙数的2倍少1,设甲数为x,则乙数可表示为( )
| A. | 2x-1 | B. | 2x+1 | C. | $\frac{1}{2}({x-1})$ | D. | $\frac{1}{2}({x+1})$ |
 如图,若AB是CD的垂直平分线,E,F是AC,AD的中点,连结BE,BF.
如图,若AB是CD的垂直平分线,E,F是AC,AD的中点,连结BE,BF.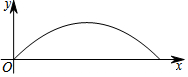 某校足球队在一次训练中,一球员从高2.4米的球门正前方m米处将球射向球门,球射向球门的路线呈抛物线,当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米,建立如图所示的平面直角坐标系
某校足球队在一次训练中,一球员从高2.4米的球门正前方m米处将球射向球门,球射向球门的路线呈抛物线,当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米,建立如图所示的平面直角坐标系