题目内容
14.如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,8),点P在边BC上以每秒1个单位长的速度由点C向点B运动,同时点Q在边AB上以每秒a个单位长的速度由点A向点B运动,运动时间为t秒(t>0).(1)若反比例函数$y=\frac{m}{x}$图象经过P点、Q点,求a的值;
(2)若△OPQ是以OQ为底的等腰直角三角形,求a的值;
(3)若OQ垂直平分AP,求a的值;
(4)当P点、Q点中一点到达B点时,PQ=2,求a的值.
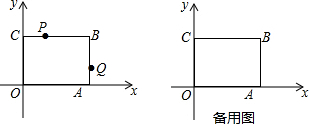
分析 (1)根据题意表示出点P、点Q的坐标,根据反比例函数图象上点的坐标特征解答;
(2)证明△OCP≌△PBQ,得到BP=OC=8,求出CP和AQ的长,计算即可;
(3)根据线段垂直平分线的性质列出算式,计算即可;
(4)分P点到达B点和Q点到达B点两种情况,根据矩形的性质解答.
解答  解:(1)∵A(10,0),C(0,8),点P在边BC上以每秒1个单位长的速度由点C向点B运动,同时点Q在边AB上以每秒a个单位长的速度由点A向点B运动,
解:(1)∵A(10,0),C(0,8),点P在边BC上以每秒1个单位长的速度由点C向点B运动,同时点Q在边AB上以每秒a个单位长的速度由点A向点B运动,
∴P(t,8),Q(10,at),
∵反比例函数y=$\frac{m}{x}$图象经过P点、Q点,
∴8t=10at,
解得a=0.8;
(2)如图(1),∵△OPQ是以OQ为底的等腰直角三角形,
∴∠OPQ=90°,OP=PQ,
∴∠OPC+∠BPQ=90°,
∵四边形OABC为矩形,
∴∠OCP=∠B=90°,
∴∠COP+∠OPC=90°,
∴∠COP=∠BPQ,
在△OCP和△PBQ中,
$\left\{\begin{array}{l}{∠OCP=∠B}\\{∠COP=∠BPQ}\\{OP=PQ}\end{array}\right.$,
∴△OCP≌△PBQ(AAS),
∴BP=OC=8,
∴CP=BC-BP=2,AQ=AB-BQ=6,
∴a=$\frac{6}{2}$=3;
(3)∵OQ垂直平分AP,
∴OP=OA,PQ=QA,
∴$\sqrt{{t}^{2}+{8}^{2}}$=10,
解得t=6,
∴Q(10,6a),P(6,8),
∵PQ=QA,
∴(10-6)2+(6a-8)2=(6a)2,
解得a=$\frac{5}{6}$;
(4)当P点到达B点,PQ=2时,AQ=8-2=6,
则a=$\frac{6}{10}$=0.6,
当Q点到达B点,PQ=2时,CP=8-2=6,AB=6,
则a=$\frac{6}{6}$=1,
答:a的值为1或0.6.
点评 本题考查的是反比例函数的应用、矩形的性质、线段垂直平分线的性质以及全等三角形的判定和性质,掌握反比例函数图象上点的坐标特征、熟记线段垂直平分线上的点到线段两端点的距离相等是解题的关键.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案 矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为( )
矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为( )| A. | (3,1) | B. | (3,$\frac{4}{3}$) | C. | (3,$\frac{5}{3}$) | D. | (3,2) |
| A. | 510×104 | B. | 51×105 | C. | 5.1×106 | D. | 0.51×107 |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{7}$ |
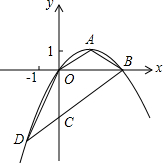 如图,顶点为A($\sqrt{3}$,1)的抛物线经过坐标原点O,与x轴交于点B.
如图,顶点为A($\sqrt{3}$,1)的抛物线经过坐标原点O,与x轴交于点B.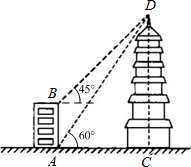 阜阳文峰塔,位于安徽阜阳城中心干道颍州路附近,于康熙三十五年(1796)建文峰塔,以振兴阜阳文风,小王在A处测得塔顶D的仰角为60°,在B处测得塔顶D的仰角为45°,其中A、C两点分别位于B、D两点正下方,且A、C两点在同一水平线上,已知AB高为13.5米,求中江塔CD的高度.(结果精确到个位)
阜阳文峰塔,位于安徽阜阳城中心干道颍州路附近,于康熙三十五年(1796)建文峰塔,以振兴阜阳文风,小王在A处测得塔顶D的仰角为60°,在B处测得塔顶D的仰角为45°,其中A、C两点分别位于B、D两点正下方,且A、C两点在同一水平线上,已知AB高为13.5米,求中江塔CD的高度.(结果精确到个位)

