题目内容
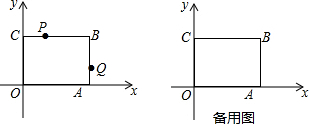
10. 矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为( )
矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为( )| A. | (3,1) | B. | (3,$\frac{4}{3}$) | C. | (3,$\frac{5}{3}$) | D. | (3,2) |
分析 如图,作点D关于直线AB的对称点H,连接CH与AB的交点为E,此时△CDE的周长最小,先求出直线CH解析式,再求出直线CH与AB的交点即可解决问题.
解答 解: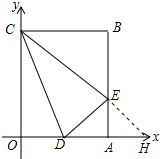 如图,作点D关于直线AB的对称点H,连接CH与AB的交点为E,此时△CDE的周长最小.
如图,作点D关于直线AB的对称点H,连接CH与AB的交点为E,此时△CDE的周长最小.
∵D($\frac{3}{2}$,0),A(3,0),
∴H($\frac{9}{2}$,0),
∴直线CH解析式为y=-$\frac{8}{9}$x+4,
∴x=3时,y=$\frac{4}{3}$,
∴点E坐标(3,$\frac{4}{3}$)
故选:B.
点评 本题考查矩形的性质、坐标与图形的性质、轴对称-最短问题、一次函数等知识,解题的关键是利用轴对称找到点E位置,学会利用一次函数解决交点问题,属于中考常考题型.

练习册系列答案
相关题目
18.下列各式,计算结果为a3的是( )
| A. | a2+a | B. | a4-a | C. | a•a2 | D. | a6÷a2 |
 请用学过的方法研究一类新函数y=$\frac{k}{{x}^{2}}$(k为常数,k≠0)的图象和性质.
请用学过的方法研究一类新函数y=$\frac{k}{{x}^{2}}$(k为常数,k≠0)的图象和性质.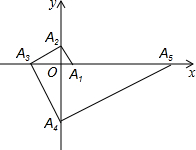 如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2016的纵坐标为-($\sqrt{3}$)2015.
如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2016的纵坐标为-($\sqrt{3}$)2015. 如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是AB∥DE.(只需写一个条件,不添加辅助线和字母)
如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是AB∥DE.(只需写一个条件,不添加辅助线和字母)