题目内容
2.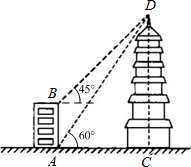 阜阳文峰塔,位于安徽阜阳城中心干道颍州路附近,于康熙三十五年(1796)建文峰塔,以振兴阜阳文风,小王在A处测得塔顶D的仰角为60°,在B处测得塔顶D的仰角为45°,其中A、C两点分别位于B、D两点正下方,且A、C两点在同一水平线上,已知AB高为13.5米,求中江塔CD的高度.(结果精确到个位)
阜阳文峰塔,位于安徽阜阳城中心干道颍州路附近,于康熙三十五年(1796)建文峰塔,以振兴阜阳文风,小王在A处测得塔顶D的仰角为60°,在B处测得塔顶D的仰角为45°,其中A、C两点分别位于B、D两点正下方,且A、C两点在同一水平线上,已知AB高为13.5米,求中江塔CD的高度.(结果精确到个位)
分析 首先分析图形,根据题意构造直角三角形.本题涉及两个直角三角形,即Rt△BED和Rt△DAC,利用已知角的正切分别计算,可得到一个关于AC的方程,从而求出DC.
解答  解:作BE⊥CD于E,
解:作BE⊥CD于E,
可得Rt△BED和矩形ACEB,
则有CE=AB=16,AC=BE,
在Rt△BED中,∠DBE=45°,DE=BE=AC,
在Rt△DAC中,∠DAC=60°,DC=ACtan60°=$\sqrt{3}$AC,
∵13.5+DE=DC,
∴13.5+AC=$\sqrt{3}$AC,
解得:AC≈18,
所以塔CD的高度为约为18米.
点评 本题考查了解直角三角形-仰角俯角问题,要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
18.下列各式,计算结果为a3的是( )
| A. | a2+a | B. | a4-a | C. | a•a2 | D. | a6÷a2 |
16.下列说法错误的是( )
| A. | 角平分线上的点到角的两边的距离相等 | |
| B. | 直角三角形斜边上的中线等于斜边的一半 | |
| C. | 菱形的对角线相等 | |
| D. | 平行四边形是中心对称图形 |
3.运用乘法公式计算(x+3)2的结果是( )
| A. | x2+9 | B. | x2-6x+9 | C. | x2+6x+9 | D. | x2+3x+9 |
11.将0.000000424用科学记数法表示为( )
| A. | 42.4×10-6 | B. | 4.24×10-7 | C. | 0.424×10-6 | D. | 42.4×10-8 |
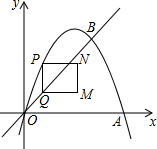 如图,在平面直角坐标系中,抛物线y=-x2+3x与x轴交于O、A两点,与直线y=x交于O、B两点,点A、B的坐标分别为(3,0)、(2,2).点P在抛物线上,且不与点O、B重合,过点P作y轴的平行线交射线OB于点Q,以PQ为边作矩形PQMN,MN与点B始终在PQ同侧,且PN=1.设点P的横坐标为m(m>0),矩形PQMN的周长为C.
如图,在平面直角坐标系中,抛物线y=-x2+3x与x轴交于O、A两点,与直线y=x交于O、B两点,点A、B的坐标分别为(3,0)、(2,2).点P在抛物线上,且不与点O、B重合,过点P作y轴的平行线交射线OB于点Q,以PQ为边作矩形PQMN,MN与点B始终在PQ同侧,且PN=1.设点P的横坐标为m(m>0),矩形PQMN的周长为C.