题目内容
19.在△ABC中,∠C=90°,点D、E分别是边BC、AC上的点,点P是一动点,连接PD、PE,∠PDB=∠1,∠PEA=∠2,∠DPE=∠α.(1)如图1所示,若点P在线段AB上,且∠α=60°,则∠1+∠2=150°(答案直接填在题中横线上);
(2)如图2所示,若点P在边AB上运动,则∠α、∠1、∠2之间的关系为有何数量关系;猜想结论并说明理由;
(3)如图3所示,若点P运动到边AB的延长线上,则∠α、∠1、∠2之间有何数量关系?请先补全图形,再猜想并直接写出结论(不需说明理由.)

分析 (1)∠DPE的邻补角为120°,∠C的邻补角为90°,由四边形的外角和可知:∠1+∠2=360°-120°-90°=150°;
(2)∠DPE的邻补角为180°-∠α,∠C的邻补角为90°,由四边形的外角和可知:∠1+∠2+90°+(180°-∠α)=360°,化简即可得出答案;
(3)根据题意画出图形可知,∠CFE是△DPF的外角,根据外角性质可知,∠CFE=∠DPE+∠PDB;另一方面,∠PEA是△CFE的外角,根据外角性质可知,∠PEA=∠C+∠CFE,根据以上两个等式即可得出∠α、∠1、∠2之间的数量关系.
解答 解:(1)150°
(2)∠DPE的邻补角为180°-∠α,
∠C的邻补角为90°,
∵∠1与∠2是四边形DPEC的外角,
∴由四边形外角和可知:∠1+∠2+90°+(180°-∠α)=360°,
∴∠1+∠2=90°+∠α
(3)如图3所示,
∠2=90°+∠α+∠1;
理由如下:设PE交BC于点F,
∴∠CFE=∠DPE+∠PDB=∠α+∠1,
∵∠PEA=∠C+∠CFE,
∴∠2=90°+∠α+∠1.
点评 本题考查四边形的外角和,涉及三角形的外角性质,综合程度较高,需要学生灵活运用所学知识.

练习册系列答案
相关题目
16.下列说法错误的是( )
| A. | 角平分线上的点到角的两边的距离相等 | |
| B. | 直角三角形斜边上的中线等于斜边的一半 | |
| C. | 菱形的对角线相等 | |
| D. | 平行四边形是中心对称图形 |
11.将0.000000424用科学记数法表示为( )
| A. | 42.4×10-6 | B. | 4.24×10-7 | C. | 0.424×10-6 | D. | 42.4×10-8 |
9.下列运算正确的是( )
| A. | x3•x2=x5 | B. | (x-1)2=x2-1 | C. | (a3)2=a9 | D. | x(x+1)=x2+1 |
 如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是AB∥DE.(只需写一个条件,不添加辅助线和字母)
如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是AB∥DE.(只需写一个条件,不添加辅助线和字母)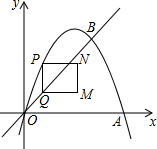 如图,在平面直角坐标系中,抛物线y=-x2+3x与x轴交于O、A两点,与直线y=x交于O、B两点,点A、B的坐标分别为(3,0)、(2,2).点P在抛物线上,且不与点O、B重合,过点P作y轴的平行线交射线OB于点Q,以PQ为边作矩形PQMN,MN与点B始终在PQ同侧,且PN=1.设点P的横坐标为m(m>0),矩形PQMN的周长为C.
如图,在平面直角坐标系中,抛物线y=-x2+3x与x轴交于O、A两点,与直线y=x交于O、B两点,点A、B的坐标分别为(3,0)、(2,2).点P在抛物线上,且不与点O、B重合,过点P作y轴的平行线交射线OB于点Q,以PQ为边作矩形PQMN,MN与点B始终在PQ同侧,且PN=1.设点P的横坐标为m(m>0),矩形PQMN的周长为C.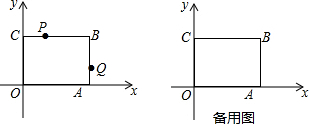
 若将两个立方体图形按如图所示的方式放置,则所构成的几何体的左视图可能是( )
若将两个立方体图形按如图所示的方式放置,则所构成的几何体的左视图可能是( )


