题目内容
20.解方程(1)(x-3)2=25(直开法)
(2)x2+3x+2=0(十字相乘法)
(3)x2-6x+8=0(配方法)
(4)x2-x-1=0(公式法)
分析 (1)直接利用开平方法解方程得出答案;
(2)直接利用十字相乘法分解因式得出答案;
(3)直接利用配方法解方程得出答案;
(4)直接利用公式法解方程得出答案.
解答 解:(1)(x-3)2=25(直开法)
x-3=±5,
解得:x1=8,x2=-2;
(2)x2+3x+2=0(十字相乘法)
(x+1)(x+2)=0,
解得:x1=-1,x2=-2;
(3)x2-6x+8=0(配方法)
(x-3)2=1,
则x-3=±1,
解得:x1=2,x2=4;
(4)x2-x-1=0(公式法)
b2-4ac=1+4=5,
则x=$\frac{1±\sqrt{5}}{2}$,
解得:x1=$\frac{1+\sqrt{5}}{2}$,x2=$\frac{1-\sqrt{5}}{2}$.
点评 此题主要考查了因式分解法以及公式法、配方法解方程,正确掌握配方法解方程是解题关键.

练习册系列答案
相关题目
10.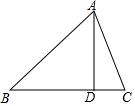 如图,在△ABC中,AD⊥BC,垂足为D,若AD=4,∠B=45°,△ABC的面积为12,则AC边的长是( )
如图,在△ABC中,AD⊥BC,垂足为D,若AD=4,∠B=45°,△ABC的面积为12,则AC边的长是( )
 如图,在△ABC中,AD⊥BC,垂足为D,若AD=4,∠B=45°,△ABC的面积为12,则AC边的长是( )
如图,在△ABC中,AD⊥BC,垂足为D,若AD=4,∠B=45°,△ABC的面积为12,则AC边的长是( )| A. | $2\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | $2\sqrt{5}$ | D. | $3\sqrt{2}$ |
11.把方程$\frac{1}{3}$x2-x-4=0左边配成一个完全平方式,得到的方程是( )
| A. | (x-$\frac{3}{2}$)2=$\frac{38}{4}$ | B. | (x-$\frac{3}{2}$)2=$\frac{38}{4}$ | C. | (x+$\frac{3}{2}$)2=$\frac{57}{4}$ | D. | (x-$\frac{3}{2}$)2=$\frac{57}{4}$ |
15.对于$\sqrt{5}$-2,下列说法中正确的是( )
| A. | 它是一个无理数 | B. | 它比0小 | ||
| C. | 它不能用数轴上的点表示出来 | D. | 它的相反数为$\sqrt{5}$+2 |
5. 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=28°,则∠2等于( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=28°,则∠2等于( )
 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=28°,则∠2等于( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=28°,则∠2等于( )| A. | 52° | B. | 60° | C. | 62° | D. | 72° |
 己知二次函数y=x2-2x-1.
己知二次函数y=x2-2x-1.