题目内容
10.如图1,在矩形ABCD和矩形CEFG中,已知$\frac{AD}{AB}$=$\frac{CG}{CE}$=k,现将图1中的矩形CEFG绕点C顺时针旋转一个角度,连结DE与AF,得到图2.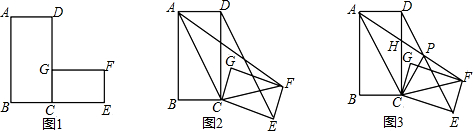
(1)如图2,当k=$\frac{1}{2}$时?求$\frac{AC}{AB}$的值;?求$\frac{AF}{DE}$的值.
(2)如图2,请直接写出$\frac{AF}{DE}$的值.(用含k的代数式表示)
(3)如图3,设DC与AF交于点H,DE与AF交于点P,连结CP,问CP与AF具有怎样的位置关系?请说明理由.
分析 (1)①由∠B=90°,$\frac{AD}{AB}$=$\frac{1}{2}$,推出AB=2BC,AC=$\sqrt{5}$BC,由此即可得出$\frac{AC}{BC}$=$\frac{\sqrt{5}}{2}$.②于$\frac{AD}{AB}$=$\frac{CG}{CE}$=k,AD=BC,CG=EF,推出$\frac{BC}{EF}$=$\frac{AB}{CE}$,于∠ABC=∠CEF=90°,推出△ABC∽△CEF,推出$\frac{AC}{CF}$=$\frac{AB}{CE}$,由AB=CD,推出$\frac{AC}{CF}$=$\frac{DC}{CE}$,由∠ACF=∠DCE,推出△ACF∽△DCE,得到$\frac{AF}{DE}$=$\frac{AC}{DC}$=$\frac{AC}{AB}$,由此即可解决问题.
(2)结论:$\frac{AF}{DE}$=$\sqrt{1+{k}^{2}}$.解法类似(1).
(3)结论:CP⊥AF.只要证明AHD∽△CHP,即可推出∠CPH=∠ADH=90°.
解答 解:(1)①如图2中,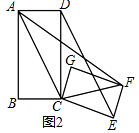
∵∠B=90°,$\frac{AD}{AB}$=$\frac{1}{2}$,
∴AB=2BC,AC=$\sqrt{5}$BC,
∴$\frac{AC}{BC}$=$\frac{\sqrt{5}}{2}$.
②∵$\frac{AD}{AB}$=$\frac{CG}{CE}$=k,AD=BC,CG=EF,
∴$\frac{BC}{EF}$=$\frac{AB}{CE}$,∵∠ABC=∠CEF=90°,
∴△ABC∽△CEF,
∴$\frac{AC}{CF}$=$\frac{AB}{CE}$,∵AB=CD,
∴$\frac{AC}{CF}$=$\frac{DC}{CE}$,∵∠ACF=∠DCE,
∴△ACF∽△DCE,
∴$\frac{AF}{DE}$=$\frac{AC}{DC}$=$\frac{AC}{AB}$=$\frac{\sqrt{5}}{2}$
(2)结论:$\frac{AF}{DE}$=$\sqrt{1+{k}^{2}}$.
理由:由(1)可知,△ACF∽△DCE,
∴$\frac{AF}{DE}$=$\frac{AC}{DC}$=$\frac{AC}{AB}$,
∵$\frac{AD}{AB}$=k,则BC=AD=k•AB,
∴AC=$\sqrt{1+{k}^{2}}$AB,
∴$\frac{AC}{AB}$=$\sqrt{1+{k}^{2}}$,
∴$\frac{AF}{DE}$=$\sqrt{1+{k}^{2}}$.
(3)结论:CP⊥AF.
理由是:如图3中,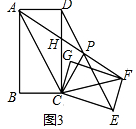
由(1)可知:△ACF∽△DCE,
∴∠CAF=∠DCE,
∵∠AHC=∠DHP,
∴△ACH∽△DPH,
∴$\frac{AH}{DH}$=$\frac{CH}{PH}$,
∴$\frac{AH}{CH}$=$\frac{DH}{PH}$,
又∵∠AHD=∠CHP,
∴△AHD∽△CHP,
∴∠CPH=∠ADH=90°,
∴CP⊥AF.
点评 本题考查相似三角形综合题、矩形的性质、勾股定理、相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形,灵活运用相似三角形的判定和性质解决问题,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案 如图,已知一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{-2}{x}$的图象交于A(-1,m),B(n,-1)两点.
如图,已知一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{-2}{x}$的图象交于A(-1,m),B(n,-1)两点. 如图,在△ABC中,AB=AC,∠BAC=120°,过点A作AB的垂线交BC于D,BC=6,则AD的长为( )
如图,在△ABC中,AB=AC,∠BAC=120°,过点A作AB的垂线交BC于D,BC=6,则AD的长为( )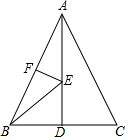 如图,在等边三角形ABC中,BC边上的高AD=6,E是高AD上的一个动点,F是边AB的中点,在点E运动的过程中,存在EB+EF的最小值,则这个最小值是( )
如图,在等边三角形ABC中,BC边上的高AD=6,E是高AD上的一个动点,F是边AB的中点,在点E运动的过程中,存在EB+EF的最小值,则这个最小值是( )