题目内容
9.如图,点A、B和线段CD都在数轴上,点A、C、D、B起始位置所表示的数分别为-2、0、3、12;线段CD沿数轴的正方向以每秒1个单位的速度移动,移动时间为t秒.(1)当t=0秒时,AC的长为2,当t=2秒时,AC的长为4.
(2)用含有t的代数式表示AC的长为t+2.
(3)当t=6秒时AC-BD=5,当t=11秒时AC+BD=15.
(4)若点A与线段CD同时出发沿数轴的正方向移动,点A的速度为每秒2个单位,在移动过程中,是否存在某一时刻使得AC=2BD,若存在,请求出t的值;若不存在,请说明理由.

分析 (1)依据A、C两点间的距离=|a-b|求解即可;
(2)t秒后点C运动的距离为t个单位长度,从而点C表示的数;根据A、C两点间的距离=|a-b|求解即可.
(3)t秒后点C运动的距离为t个单位长度,点D运动的距离为t个单位长度,从而可得到点A、点D表示的数;根据两点间的距离=|a-b|表示出AC、BD,.根据AC-BD=5和AC+BD=15得到关于t的含绝对值符号的一元一次方程,分别解方程即可得出结论;
(4)假设能够相等,找出AC、BD,根据AC=2BD即可列出关于t的含绝对值符号的一元一次方程,解方程即可得出结论.
解答 解:(1)当t=0秒时,AC=|-2-0|=|-2|=2;
当t=2秒时,移动后C表示的数为2,
∴AC=|-2-2|=4.
故答案为:2;4.
(2)点A表示的数为-2,点C表示的数为t;
∴AC=|-2-t|=t+2.
故答案为t+2.
(3)∵t秒后点C运动的距离为t个单位长度,点D运动的距离为t个单位长度,
∴C表示的数是t,D表示的数是3+t,
∴AC=t+2,BD=|12-(3+t)|,
∵AC-BD=5,
∴t+2-|12-(t+3)|=5.
解得:t=6.
∴当t=6秒时AC-BD=5;
∵AC+BD=15,
∴t+2+|12-(t+3)|=15,
t=11;
当t=11秒时AC+BD=15,
故答案为6,11;
(4)假设能相等,则点A表示的数为2t-2,C表示的数为t,D表示的数为t+3,B表示的数为12,
∴AC=|2t-2-t|=|t-2|,BD=|t+3-12|=|t-9|,
∵AC=2BD,
∴|t-2|=2|t-9|,
解得:t1=16,t2=$\frac{20}{3}$.
故在运动的过程中使得AC=2BD,此时运动的时间为16秒和$\frac{20}{3}$秒.
点评 本题考查了数轴以及一元一次方程的应用,根据数量关系列出一元一次方程是解题的关键.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案| A. | M>N | B. | M<N | C. | M=N | D. | 无法确定 |
| A. | 2cm | B. | 3cm | C. | 9cm | D. | 10cm |
 长方形如图折叠,已知∠AEB′=56°,则∠BEF=62度.
长方形如图折叠,已知∠AEB′=56°,则∠BEF=62度.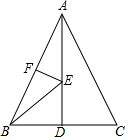 如图,在等边三角形ABC中,BC边上的高AD=6,E是高AD上的一个动点,F是边AB的中点,在点E运动的过程中,存在EB+EF的最小值,则这个最小值是( )
如图,在等边三角形ABC中,BC边上的高AD=6,E是高AD上的一个动点,F是边AB的中点,在点E运动的过程中,存在EB+EF的最小值,则这个最小值是( )