题目内容
16.计算(1)(2a-1b3)2•($\frac{1}{2}$ab-2)3;
(2)(1+$\frac{4}{{a}^{2}-4}$)÷$\frac{a}{a-2}$.
分析 (1)根据积的乘方和同底数幂的乘法进行计算即可;
(2)先化简括号内的式子再与括号外的式子相除,将除法转化为乘法进行计算即可.
解答 解:(1)(2a-1b3)2•($\frac{1}{2}$ab-2)3
=$4{a}^{-2}{b}^{6}×\frac{1}{8}{a}^{3}{b}^{-6}$
=$\frac{1}{2}a$;
(2)(1+$\frac{4}{{a}^{2}-4}$)÷$\frac{a}{a-2}$
=$\frac{{a}^{2}-4+4}{(a+2)(a-2)}×\frac{a-2}{a}$
=$\frac{{a}^{2}}{(a+2)(a-2)}×\frac{a-2}{a}$
=$\frac{a}{a+2}$.
点评 本题考查分式的混合运算、负整数指数幂,解题的关键是明确它们各自的计算方法,运用转化的数学思想将除法转化为乘法进行计算.

练习册系列答案
相关题目
18.估算$\sqrt{4}$+$\sqrt{15}$÷$\sqrt{3}$的运算结果应在( )
| A. | 1到2之间 | B. | 2到3之间 | C. | 3到4之间 | D. | 4到5之间 |
19.下列运算正确的是( )
| A. | a+2a=2a2 | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | (x-3)2=x2-9 | D. | -2-2=-$\frac{1}{4}$ |
 已知:如图,在△AOB中,OB=OA,∠AOB=90°.在△ACQ中,AC=CQ,∠ACQ=90°,点P为BQ的中点
已知:如图,在△AOB中,OB=OA,∠AOB=90°.在△ACQ中,AC=CQ,∠ACQ=90°,点P为BQ的中点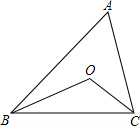 如图,∠ABC=40°,∠ACB=60°,BO、CO平分∠ABC和∠ACB,则∠BOC=130°.
如图,∠ABC=40°,∠ACB=60°,BO、CO平分∠ABC和∠ACB,则∠BOC=130°.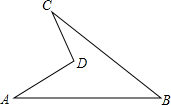 如图是一块地,已知AD=4m,CD=3m,AB=13m,BC=12m,且CD⊥AD,求这块地的面积.
如图是一块地,已知AD=4m,CD=3m,AB=13m,BC=12m,且CD⊥AD,求这块地的面积.