题目内容
6.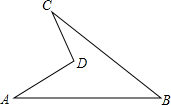 如图是一块地,已知AD=4m,CD=3m,AB=13m,BC=12m,且CD⊥AD,求这块地的面积.
如图是一块地,已知AD=4m,CD=3m,AB=13m,BC=12m,且CD⊥AD,求这块地的面积.
分析 连接AC,利用勾股定理可以得出三角形ACD和ABC是直角三角形,△ABC的面积减去△ACD的面积就是所求的面积.
解答  解:连接AC,
解:连接AC,
∵CD⊥AD
∴∠ADC=90°,
∵AD=4,CD=3,
∴AC2=AD2+CD2=42+32=25,
又∵AC>0,
∴AC=5,
又∵BC=12,AB=13,
∴AC2+BC2=52+122=169,
又∵AB2=169,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴S四边形ABCD=S△ABC-S△ADC=30-6=24m2.
点评 本题主要考查勾股定理和勾股定理逆定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
17.-$\frac{4}{5}$的相反数是( )
| A. | -$\frac{4}{5}$ | B. | $\frac{5}{4}$ | C. | -$\frac{5}{4}$ | D. | $\frac{4}{5}$ |
14.下列二次根式中,是最简二次根式的是( )
| A. | $\sqrt{0.2b}$ | B. | $\sqrt{12a-12b}$ | C. | $\sqrt{x2-y2}$ | D. | $\sqrt{5ab2}$ |
11.如果一个四边形的两条对角线互相垂直平分且相等,那么这个四边形是( )
| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 都有可能 |
 已知抛物线y=x2-2x-3
已知抛物线y=x2-2x-3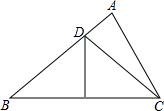 如图,△ABC中,∠A=80°,∠B=40°,BC的垂直平分线交AB于点D,连结DC,如果AD=3,BD=8,那么△ADC的周长为19.
如图,△ABC中,∠A=80°,∠B=40°,BC的垂直平分线交AB于点D,连结DC,如果AD=3,BD=8,那么△ADC的周长为19.