题目内容
1.先化简,再求值(1)(2a+b)2-(2a-b)(a+b)-2(a-2b)(a+2b),其中a=$\frac{1}{2}$,b=-2.
(2)[(x+2y)2-(x+y)(3x-y)-5y2]÷2x,其中x=-2,y=$\frac{1}{2}$.
分析 (1)利用完全平方公式、平方差公式与整式的乘法计算,进一步合并化简后,代入数值求得答案即可;
(2)利用完全平方公式、平方差公式与整式的乘法计算,进一步合并化简后,再算除法,最后代入求得数值即可.
解答 解:(1)原式=4a2+4ab+b2-2a2-ab+b2-2a2+8b2
=3ab+10b2
当a=$\frac{1}{2}$,b=-2时,
原式=3×$\frac{1}{2}$×(-2)+10×(-2)2=37.
(2)原式=[x2+4xy+4y2-3x2-2xy+y2-5y2]÷2x
=[-2x2+2xy]÷2x
=-x+y
当x=-2,y=$\frac{1}{2}$时,
原式=2+$\frac{1}{2}$=$\frac{5}{2}$.
点评 此题考查了整式的化简求值与整式的混合运算,主要考查了完全平方公式、平方差公式、合并同类项的知识点.注意运算顺序以及符号的处理.

练习册系列答案
相关题目
3.据统计,2015年湖南省旅游总收入3713亿元,把3713亿这个数字用科学记数法表示为( )
| A. | 3713×l08 | B. | 3.713×1010 | C. | 3.713×1011 | D. | 3.713×1012 |
4.已知m=8-$\sqrt{20}$,估算m的值所在的范围是( )
| A. | 1<m<2 | B. | 2<m<3 | C. | 3<m<4 | D. | 4<m<5 |
13.下列因式分解正确的是( )
| A. | x3-x=x(x2-1) | B. | a2-8a+16=(a-4)2 | C. | 5x2+5y2=5(x+y)2 | D. | m2+m-6=(m-3)(m+2) |
11.如果一个四边形的两条对角线互相垂直平分且相等,那么这个四边形是( )
| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 都有可能 |
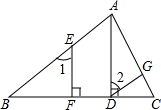 如图,已知AD⊥BC,EF⊥BC,∠1=∠2.求证:DG∥BA.
如图,已知AD⊥BC,EF⊥BC,∠1=∠2.求证:DG∥BA.