已知x=1是方程$\frac{ax+3}{2}=1-\frac{x-a}{3}$的解.则a=-5．题目和参考答案——青夏教育精英家教网—

题目内容

1．已知x=1是方程$\frac{ax+3}{2}=1-\frac{x-a}{3}$的解，则a=-5．

分析把x=1代入方程计算，即可求出a的值．

解答解：把x=1代入方程得：$\frac{a+3}{2}$=1-$\frac{1-a}{3}$，
去分母得：3a+9=6-2+2a，
移项合并得：a=-5．
故答案为：-5．

点评此题考查了一元一次方程的解，方程的解即为能使方程左右两边相等的未知数的值．

练习册系列答案

相关题目

16．

如图，直角三角形ABC中，∠ACB=90°，AB=10，BC=6，在线段AB上取一点D，作DF⊥AB交AC于点F，现将△ADF沿DF折叠，使点A落在线段DB上，对应点记为H，AD的中点E的对应点记为G，若△GFH∽△GBF，则AD=$\frac{16}{5}$．

17．点E是△ABC的重心，$\overrightarrow{AB}=\overrightarrow a$，$\overrightarrow{AC}=\overrightarrow b$，那么$\overrightarrow{BE}$=$\frac{1}{3}\overrightarrow b-\frac{2}{3}\overrightarrow a$（用$\overrightarrow a$、$\overrightarrow b$表示）

9．要登上某建筑物，靠墙有一架梯子，底端离建筑物3m，顶端离地面4m，则梯子的长度为（　　）

16．已知n是使$\sqrt{27n}$的值为整数的最小正整数，估算$\sqrt{n}$的值，下列说法正确的是（　　）

6．甲、乙两艘客轮同时离开港口，航行的速度都是40m/min，甲客轮用15min到达点A，乙客轮用20min到达点B．若A，B两点的直线距离为1000m，甲客轮沿着北偏东30°的方向航行，则乙客轮的航行方向可能是南偏东60°或北偏西60°．

13．

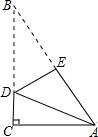一张直角三角形的纸片，像图中那样折叠，使两个锐角顶点A、B重合，若∠B=30°，AC=$\sqrt{3}$，则折痕DE的长等于（　　）

10．

在如图所示的5×5方格纸中，点A、B在边长为1小正方形的格点上，点C也在正方形的格点上．已知△ABC面积为2，在图中的方格纸中，满足条件的C点有5个．

11．下列命题中，逆命题成立的是（　　）

	A．	两个全等三角形的对应角相等
	B．	如果两个实数是正数，那么它们的积是正数
	C．	如果三角形的三边长a，b，c满足a²+b²=c²，那么这个三角形是直角三角形
	D．	如果两个角是直角，那么它们相等

试题分类