题目内容
10.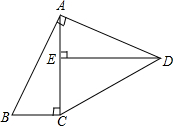 如图,在四边形ABCD中,∠BAD=∠ACB=∠AED=90°,AB=AD.
如图,在四边形ABCD中,∠BAD=∠ACB=∠AED=90°,AB=AD.(1)求证:AC=DE;
(2)若AC=4BC,CD=5,求四边形ABCD的面积.
分析 (1)由余角的性质得到∠B=∠DAE,根据全等三角形的性质即可得到结论;
(2)根据全等三角形的性质得到BC=AE,根据勾股定理得到BC=1,CE=3,AC=DE=4,由三角形的面积公式即可得到结论.
解答 (1)证明:∵∠BAD=∠ACB=∠AED=90°,
∴∠B+∠BAC=∠BAC+∠DAE=90°,
∴∠B=∠DAE,
在△ABC与△ADE中,$\left\{\begin{array}{l}{∠B=∠ADE}\\{∠ACB=∠AED}\\{AB=AD}\end{array}\right.$,
∴△ABC≌△ADE,
∴AC=DE;
(2)解:∵△ABC≌△ADE,
∴BC=AE,
∵AC=4BC,
∴CE=3BC,
∵DE2+CE2=CD2,
即(4BC)2+(3BC)2=52,
∴BC=1,CE=3,AC=DE=4,
∴四边形ABCD的面积=S△ABC+S△ADE+S△CDE=$\frac{1}{2}$×1×4+$\frac{1}{2}$×1×4+$\frac{1}{2}$×3×4=10.
点评 本题考查了全等三角形的判断和性质,勾股定理,三角形的面积的计算,熟练掌握全等三角形的判断和性质是解题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
2.有3张边长为a的正方形纸片,4张边长分别为a、b(b<a)的长方形纸片,5张边长为b的正方形纸片,从其中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(按原纸张进行无空隙、无重叠拼接),则拼成的正方形的边长最长可以为( )
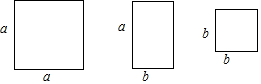

| A. | a+b | B. | 2a+b | C. | 2a-b | D. | a+2b |
20.已知a、b为实数,且$\sqrt{a-\frac{1}{2}}$+b2+4=4b,则a2015b2016的值是( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
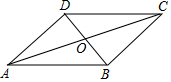 如图,在?ABCD中,对角线AC,BD相交于点O,AD=3$\sqrt{3}$,BD=6,AC=12,则?ABCD的面积是18$\sqrt{3}$.
如图,在?ABCD中,对角线AC,BD相交于点O,AD=3$\sqrt{3}$,BD=6,AC=12,则?ABCD的面积是18$\sqrt{3}$.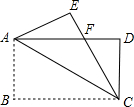 如图,将矩形ABCD沿对角线AC对折,使△ABC落在△ACE的位置,且CE与AD相交于点F,连结ED,若AB=$\sqrt{3}$,BC=3.
如图,将矩形ABCD沿对角线AC对折,使△ABC落在△ACE的位置,且CE与AD相交于点F,连结ED,若AB=$\sqrt{3}$,BC=3.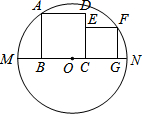 如图,两个正方形都在⊙O的直径MN的同侧,顶点B、C、G都在MN上,正方形ABCD的顶点A和正方形CEFG的顶点F都在⊙O上,点E在CD上.若AB=5,FG=3,则OC的长为2.
如图,两个正方形都在⊙O的直径MN的同侧,顶点B、C、G都在MN上,正方形ABCD的顶点A和正方形CEFG的顶点F都在⊙O上,点E在CD上.若AB=5,FG=3,则OC的长为2.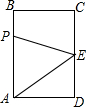 如图,长方形ABCD中,AB=4cm,BC=3cm,E为CD的中点.动点P从A点出发,以每秒1cm的速度沿A-B-C-E运动,最终到达点E.若点P运动的时间为x秒,则当x=$\frac{10}{3}$或5时,△APE的面积等于5.
如图,长方形ABCD中,AB=4cm,BC=3cm,E为CD的中点.动点P从A点出发,以每秒1cm的速度沿A-B-C-E运动,最终到达点E.若点P运动的时间为x秒,则当x=$\frac{10}{3}$或5时,△APE的面积等于5.