题目内容
12.设关于x的方程x2-2x-m+1=0的两个实数根分别为α,β,若|α|+|β|=6,那么实数m的取值范围是9.分析 根据根与系数的关系得α+β=2,αβ=-m+1,由|α|+|β|=6,推得αβ<0,由α+β=2得α2+β2=4-αβ,由|α|+|β|=6得α2+β2=36-|αβ|,于是4-αβ=36-|αβ|=36+αβ,从而得到αβ=-8,即-m+1=-8,解方程即可求得结论.
解答 解:∵关于x的方程x2-2x-m+1=0的两个实数根分别为α,β,
∴α+β=2,αβ=-m+1,
∵|α|+|β|=6,
∴α,β为异号,
即αβ<0,
由α+β=2得α2+β2=4-αβ,
由|α|+|β|=6得α2+β2=36-|αβ|,
∴4-αβ=36-|αβ|=36+αβ,
∴αβ=-8,
∴-m+1=-8,
∴m=9,
故答案为:9.
点评 此题主要考查了根与系数的关系,能根据根与系数的关系与与已知条件求得αβ<0是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
7.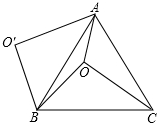 如图,O是等边△ABC内一点,OA=6,OB=8,OC=10,以B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:①△BO′A可以由△BOC绕点B逆时针方向旋转60°得到;②连接OO′,则OO′=8;③∠AOB=150°;④${S_{四边形AOBO'}}=24+12\sqrt{3}$
如图,O是等边△ABC内一点,OA=6,OB=8,OC=10,以B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:①△BO′A可以由△BOC绕点B逆时针方向旋转60°得到;②连接OO′,则OO′=8;③∠AOB=150°;④${S_{四边形AOBO'}}=24+12\sqrt{3}$
其中正确的有( )
 如图,O是等边△ABC内一点,OA=6,OB=8,OC=10,以B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:①△BO′A可以由△BOC绕点B逆时针方向旋转60°得到;②连接OO′,则OO′=8;③∠AOB=150°;④${S_{四边形AOBO'}}=24+12\sqrt{3}$
如图,O是等边△ABC内一点,OA=6,OB=8,OC=10,以B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:①△BO′A可以由△BOC绕点B逆时针方向旋转60°得到;②连接OO′,则OO′=8;③∠AOB=150°;④${S_{四边形AOBO'}}=24+12\sqrt{3}$其中正确的有( )
| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
17.下列四个命题中,正确的个数有( )
①圆的对称轴是直径;
②经过三点可以确定一个圆;
③三角形的外心到三角形各顶点的距离都相等;
④半径相等的两个半圆是等弧;
⑤平分弦的直径垂直于弦.
①圆的对称轴是直径;
②经过三点可以确定一个圆;
③三角形的外心到三角形各顶点的距离都相等;
④半径相等的两个半圆是等弧;
⑤平分弦的直径垂直于弦.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.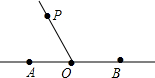 如图,已知∠AOB=180°,则下列语句中,描述错误的是( )
如图,已知∠AOB=180°,则下列语句中,描述错误的是( )
 如图,已知∠AOB=180°,则下列语句中,描述错误的是( )
如图,已知∠AOB=180°,则下列语句中,描述错误的是( )| A. | 点O在直线AB上 | B. | 直线AB与直线OP相交于点O | ||
| C. | 点P在直线AB上 | D. | ∠AOP与∠BOP互为补角 |
2.已知点(-1,y1),(2,y2),$({\sqrt{5},{y_3}})$在反比例函数y=-$\frac{{{k^2}+1}}{x}$的图象上,则下列关系式正确的是( )
| A. | y3<y2<y1 | B. | y2<y3<y1 | C. | y3<y1<y2 | D. | y2<y1<y3 |
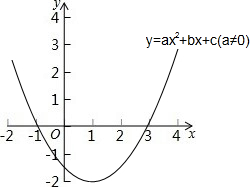 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0,②当-1≤x≤3时,y<0,③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2,④9a+3b+c=0,其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0,②当-1≤x≤3时,y<0,③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2,④9a+3b+c=0,其中正确的是( )