题目内容
2.已知:?ABCD,A、E、F共线,B、C、F共线,则:(1)与△FCE相似的三角形有△EBA与△ADF;
(2)若CE=1,CD=3,CF=2,AE=3,则△ABF的周长为13.5.
分析 (1)根据平行四边形的性质得到AB∥CD,AD∥BC,然后根据平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似可判断△ECF∽△EBA,△ADF∽△ECF;
(2)由四边形ABCD是平行四边形,得出△ECF∽△EDA,得出两个比例式$\frac{CF}{DA}=\frac{EC}{ED}$,$\frac{EF}{AE}=\frac{EC}{ED}$,求出线段DA,EF,即可求出△ABF的周长.
解答 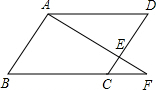 解:(1)∵四边形ABCD为平行四边形,
解:(1)∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC,
∵CF∥AB,
∴△ECF∽△EBA,
∵AD∥CE,
∴△ADF∽△ECF,
故答案为:△EBA与△ADF;
(2)解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠F=∠EAD,∠FCE=∠EDA,
∴△ECF∽△EDA,
∴$\frac{CF}{DA}=\frac{EC}{ED}$,$\frac{EF}{AE}=\frac{EC}{ED}$,
∵CE=1,CD=3,
∴ED=CD-CE=3-1=2
∵CF=2,AE=3,
∴$\frac{2}{DA}$=$\frac{1}{2}$,解得DA=4,$\frac{EF}{3}=\frac{1}{2}$,EF=1.5
∴△ABF的周长=AB+BC+CF+FE+AE=3+4+2+1.5+3=13.5.
故答案为:13.5.
点评 本题考查了相似三角形的判定:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似.也考查了平行四边形的性质.

练习册系列答案
相关题目
1.若m、n是一元二次方程x2-5x+2=0的两个实数根,则m+n-mn的值是( )
| A. | 7 | B. | -7 | C. | 3 | D. | -3 |
2.若a是(-4)2的平方根,b的一个平方根是2,则a+b的值为( )
| A. | 0 | B. | 8 | C. | 0或8 | D. | 0或-8 |
19.以下列长度的各组线段为边,不能构成三角形的是( )
| A. | 3,4,8 | B. | 15,20,8 | C. | 9,15,8 | D. | 4,9,6 |
14.下列图形中,是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
11.下列等式由左边到右边的变形中,属于因式分解的是( )
| A. | 6ab=2a•3b | B. | x2-4+3x=(x+2)( x-2)+3x | ||
| C. | x2-9=( x+3)( x-3) | D. | (x+2)( x-2)=x2-4 |