题目内容
1.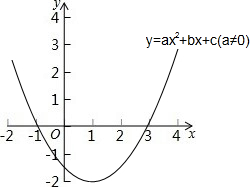 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0,②当-1≤x≤3时,y<0,③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2,④9a+3b+c=0,其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0,②当-1≤x≤3时,y<0,③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2,④9a+3b+c=0,其中正确的是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据抛物线的对称轴判断①,由图象判断②,根据抛物线的性质判断③,根据x=3时,y=0判断④.
解答 解:①由图象可知,抛物线的对称轴是x=1,
∴-$\frac{b}{2a}$=1,即2a+b=0,①正确;
②由图象可知,当-1<x<3时,y<0,②错误;
③在对称轴左侧,当x1<x2时,y1>y2,
在对称轴右侧,当x1<x2时,y1<y2,③错误;
④当x=3时,y=0,
∴9a+3b+c=0,④正确,
故选:B.
点评 本题考查的是二次函数图象与系数的关系,二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
11.下列等式由左边到右边的变形中,属于因式分解的是( )
| A. | 6ab=2a•3b | B. | x2-4+3x=(x+2)( x-2)+3x | ||
| C. | x2-9=( x+3)( x-3) | D. | (x+2)( x-2)=x2-4 |
11.x2+2ax+16是一个完全平方式,则a的值为( )
| A. | 4或-4 | B. | 8 | C. | 4 | D. | 8或-8 |
 如图,将一长方形纸条折叠后,若∠1=70°,则∠2=55°.
如图,将一长方形纸条折叠后,若∠1=70°,则∠2=55°. 如图,已知直线a∥b,直线l与直线a相交于点P,与直线b相交于点Q,且MP⊥直线l,若∠1=58°,则∠2的度数为32°.
如图,已知直线a∥b,直线l与直线a相交于点P,与直线b相交于点Q,且MP⊥直线l,若∠1=58°,则∠2的度数为32°.