题目内容
11.对于实数a,b,我们定义符号max{a,b}的意义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b]=b;如:max{4,-2}=4,max{3,3}=3,若关于x的函数为y=max{x+3,-x+1},则该函数的最小值是( )| A. | 0 | B. | 2 | C. | 3 | D. | 4 |
分析 分x≥-1和x<-1两种情况进行讨论计算,
解答 解:当x+3≥-x+1,
即:x≥-1时,y=x+3,
∴当x=-1时,ymin=2,
当x+3<-x+1,
即:x<-1时,y=-x+1,
∵x<-1,
∴-x>1,
∴-x+1>2,
∴y>2,
∴ymin=2,
故选B
点评 此题是分段函数题,主要考查了新定义,解本题的关键是分段.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
1. 如图,AB是⊙O的直径,CD是⊙O上的点,∠DCB=30°,过点D作⊙O的切线交AB的延长线于E,若AB=4,则DE的长为( )
如图,AB是⊙O的直径,CD是⊙O上的点,∠DCB=30°,过点D作⊙O的切线交AB的延长线于E,若AB=4,则DE的长为( )
 如图,AB是⊙O的直径,CD是⊙O上的点,∠DCB=30°,过点D作⊙O的切线交AB的延长线于E,若AB=4,则DE的长为( )
如图,AB是⊙O的直径,CD是⊙O上的点,∠DCB=30°,过点D作⊙O的切线交AB的延长线于E,若AB=4,则DE的长为( )| A. | 2 | B. | 4 | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
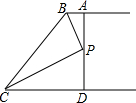 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( ) 如图,点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF,求证:AB∥DE.
如图,点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF,求证:AB∥DE. 证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.