题目内容
1. 如图,AB是⊙O的直径,CD是⊙O上的点,∠DCB=30°,过点D作⊙O的切线交AB的延长线于E,若AB=4,则DE的长为( )
如图,AB是⊙O的直径,CD是⊙O上的点,∠DCB=30°,过点D作⊙O的切线交AB的延长线于E,若AB=4,则DE的长为( )| A. | 2 | B. | 4 | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
分析 连接OD.由同弧所对的圆心角是圆周角的2倍可求得∠BOD=60°,然后由切线的性质可证明∠ODE=90°,根据三角形的内角和是180°可求得∠E=30°,依据含30°直角三角形的性质可知OE=2OD=4,再利用勾股定理,即可解答.
解答 解:如图,连接OD.
∵∠DCB=30°,
∴∠BOD=60°.
∵DE是⊙O的切线,
∴∠ODE=90°.
∴∠DEO=30°.
∴OE=2OD=AB=4,
在Rt△ODE中,DE=$\sqrt{O{E}^{2}-O{D}^{2}}=\sqrt{{4}^{2}-{2}^{2}}=2\sqrt{3}$.
点评 本题主要考查的是切线的性质、圆周角定理、含30°直角三角形的性质,证得△ODE为含30°的直角三角形是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
11. 如图,已知菱形ABCD对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是( )
如图,已知菱形ABCD对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是( )
 如图,已知菱形ABCD对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是( )
如图,已知菱形ABCD对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是( )| A. | 5$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | $\frac{24}{5}$ | D. | $\frac{48}{5}$ |
12.若二次函数y=x2-6x+9的图象经过A(-1,y1),B(1,y2),C(3+$\sqrt{3}$,y3)三点.则关于y1,y2,y3大小关系正确的是( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y2>y1>y3 | D. | y3>y1>y2 |
9.已知△ABC∽△DEF,且周长之比为1:9,则△ABC与△DEF的高的比为( )
| A. | 1:3 | B. | 1:9 | C. | 1:18 | D. | 1:81 |
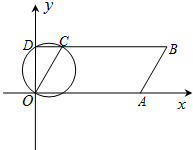 如图,在平面直角坐标系中,以OC为直径的圆交y轴于点D,∠DOC=30°,OC=2.延长DC至点B,使得CB=4DC,过B点作BA∥OC交x轴于A点.
如图,在平面直角坐标系中,以OC为直径的圆交y轴于点D,∠DOC=30°,OC=2.延长DC至点B,使得CB=4DC,过B点作BA∥OC交x轴于A点.