题目内容

6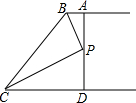．如图，AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直．若AD=8，则点P到BC的距离是（　　）
A．8B．6C．4D．2

分析 过点P作PE⊥BC于E，根据角平分线上的点到角的两边的距离相等可得PA=PE，PD=PE，那么PE=PA=PD，又AD=8，进而求出PE=4．

解答 解：过点P作PE⊥BC于E，
∵AB∥CD，PA⊥AB，
∴PD⊥CD，
∵BP和CP分别平分∠ABC和∠DCB，
∴PA=PE，PD=PE，
∴PE=PA=PD，
∵PA+PD=AD=8，
∴PA=PD=4，
∴PE=4．
故选C．

点评 本题考查了角平分线上的点到角的两边的距离相等的性质，熟记性质并作辅助线是解题的关键．

练习册系列答案
相关题目
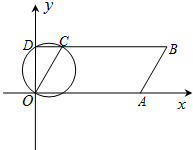16．如图，在平面直角坐标系中，以OC为直径的圆交y轴于点D，∠DOC=30°，OC=2．延长DC至点B，使得CB=4DC，过B点作BA∥OC交x轴于A点．
（1）请求出BC的长度；
（2）若P点与B点是关于直线AC的对称点，试求出点P的坐标；
（3）若点M、N分别为CB、AB上的动点，P点与B点是关于直线MN的对称点，过点P作x轴的平行线，与AC、OC分别交于点E、F．若PE﹕PF=1：3，点P的横坐标为m．请求出点P的纵坐标，并直接写出m的取值范围．
17．已知△ABC是等腰直角三角形，AC=BC=2，D是边AB上一动点（A、B两点除外），将△CAD绕点C按逆时针方向旋转角α得到△CEF，其中点E是点A的对应点，点F是点D的对应点．

（1）如图1，当α=90°时，G是边AB上一点，且BG=AD，连接GF．求证：GF∥AC；
（2）如图2，当90°≤α≤180°时，AE与DF相交于点M．
①当点M与点C、D不重合时，连接CM，求∠CMD的度数；
②设D为边AB的中点，当α从90°变化到180°时，求点M运动的路径长．
14．正方形ABCD边长为4，M、N分别是BC、CD上的两个动点，当M点在BC上运动时，保持AM和MN垂直，
（1）证明：Rt△ABM∽Rt△MCN；
（2）设BM=x，梯形ABCN的面积为y，求y与x之间的函数关系式；当M点运动到什么位置时，四边形ABCN面积最大，并求出最大面积；
（3）当M点运动到什么位置时Rt△ABM∽Rt△AMN，求x的值．
1．化简求值：$\frac{x}{{x}^{2}-1}$$÷\frac{{x}^{2}+x}{{x}^{2}+2x+1}$-$\frac{{x}^{2}}{x-1}$．
11．对于实数a，b，我们定义符号max{a，b}的意义为：当a≥b时，max{a，b}=a；当a＜b时，max{a，b]=b；如：max{4，-2}=4，max{3，3}=3，若关于x的函数为y=max{x+3，-x+1}，则该函数的最小值是（　　）
A．0B．2C．3D．4
18．下列四个立体图形中，它们各自的三视图都相同的是（　　）
A．B．C．D．
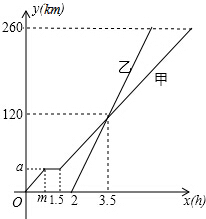15．甲、乙两车从A地驶向B地，并以各自的速度匀速行驶，甲车比乙车早行驶2h，并且甲车途中休息了0.5h，如图是甲乙两车行驶的距离y（km）与时间x（h）的函数图象．则下列结论：
（1）a=40，m=1；
（2）乙的速度是80km/h；
（3）甲比乙迟$\frac{7}{4}$h到达B地；
（4）乙车行驶$\frac{9}{4}$小时或$\frac{19}{4}$小时，两车恰好相距50km．
正确的个数是（　　）
A．1B．2C．3D．4
16．已知一次函数y=kx+b-x的图象与x轴的正半轴相交，且函数值y随自变量x的增大而增大，则k，b的取值情况为（　　）
A．k＞1，b＜0B．k＞1，b＞0C．k＞0，b＞0D．k＞0，b＜0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网