题目内容
1. 证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.已知:如图,∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB
求证:PD=PE.
请你补全已知和求证,并写出证明过程.
分析 根据图形写出已知条件和求证,利用全等三角形的判定得出△PDO≌△PEO,由全等三角形的性质可得结论.
解答 解:已知:PD⊥OA,PE⊥OB,垂足分别为D、E;求证:PD=PE.
故答案为:PD=PE.
∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°,
在△PDO和△PEO中,
$\left\{\begin{array}{l}{∠PDO=∠PEO}\\{∠AOC=∠BOC}\\{OP=OP}\end{array}\right.$,
∴△PDO≌△PEO(AAS),
∴PD=PE.
点评 本题主要考查了角平分线的性质和全等三角形的性质及判定,利用图形写出已知条件和求证是解答此题的关键.

练习册系列答案
相关题目
9.我国药学家屠呦呦荣获2015年诺贝尔医学奖,其突出贡献是在东晋葛洪《肘后备急方•治寒热诸症方》的启发下.创制了新型抗疟药一青蒿素.她获得的奖金为400万瑞典克朗,约合300万人民币.“300万”可用科学记数法表示为( )
| A. | 3×107 | B. | 0.3×107 | C. | 3×106 | D. | 30×105 |
16.已知一次函数y=kx+b-x的图象与x轴的正半轴相交,且函数值y随自变量x的增大而增大,则k,b的取值情况为( )
| A. | k>1,b<0 | B. | k>1,b>0 | C. | k>0,b>0 | D. | k>0,b<0 |
6. 如图是某几何体的三视图,该几何体是( )
如图是某几何体的三视图,该几何体是( )
 如图是某几何体的三视图,该几何体是( )
如图是某几何体的三视图,该几何体是( )| A. | 球 | B. | 三棱柱 | C. | 圆柱 | D. | 圆锥 |
10.在△ABC中,若∠A=95°,∠B=40°,则∠C的度数为( )
| A. | 35° | B. | 40° | C. | 45° | D. | 50° |
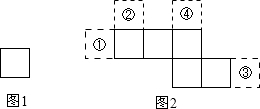
 如图中的四边形均为矩形,根据图形,写出一个正确的等式am+bm+cm=m(a+b+c).
如图中的四边形均为矩形,根据图形,写出一个正确的等式am+bm+cm=m(a+b+c).