题目内容
17.先化简,再求值:(1-$\frac{1}{a+1}$)÷$\frac{a}{{a}^{2}+2a+1}$,其中a=$\sqrt{2}$-1.分析 先把括号内通分和除法运算化为乘法运算,然后把分子因式分解后约分得到原式=a+1,再把a的值代入计算即可.
解答 解:原式=$\frac{a+1-1}{a+1}$•$\frac{(a+1)^{2}}{a}$
=a+1,
当a=$\sqrt{2}$-1时,原式=$\sqrt{2}$-1+1=$\sqrt{2}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
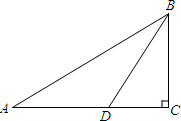 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,tan A=$\frac{\sqrt{3}}{3}$,AD=20.求BC的长.
如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,tan A=$\frac{\sqrt{3}}{3}$,AD=20.求BC的长.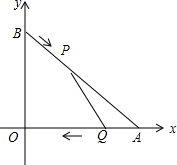 如图,A,B两点的坐标分别是(8,0),(0,6),点P由点B出发沿BA方向向点A做匀速直线运动,速度为每秒3个单位长度,同时,点Q由A出发沿AO(O为坐标原点)方向向点O做匀速直线运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<$\frac{10}{3}$)秒,解答如下问题:设△AQP的面积为S个平方单位,求S与t之间的函数关系式,并求出S的最大值.
如图,A,B两点的坐标分别是(8,0),(0,6),点P由点B出发沿BA方向向点A做匀速直线运动,速度为每秒3个单位长度,同时,点Q由A出发沿AO(O为坐标原点)方向向点O做匀速直线运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<$\frac{10}{3}$)秒,解答如下问题:设△AQP的面积为S个平方单位,求S与t之间的函数关系式,并求出S的最大值.