题目内容
5.方程2x+y=9在正整数范围内的解有4个,它们是$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$,$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$,$\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$,$\left\{\begin{array}{l}{x=1}\\{y=7}\end{array}\right.$.分析 要求方程2x+y=9在正整数范围内的解,首先将方程做适当变形,用x表示y,再进一步根据解为正整数,确定其中一个未知数的值,从而求得另一个未知数的值.
解答 解:由题意,得x=$\frac{9-y}{2}$,
要使x,y都是正整数,则合适的y的值只能是y=1,3,5,7,
相应的x的值为x=4,3,2,1.
故答案为4,$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$,$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$,$\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$,$\left\{\begin{array}{l}{x=1}\\{y=7}\end{array}\right.$.
点评 本题是求不定方程的整数解,先将方程做适当变形,然后列举出适合条件的所有整数值,再求出另一个未知数的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.若a>b,则不等式组$\left\{\begin{array}{l}{x<a+1}\\{x<b+1}\end{array}\right.$的解集是( )
| A. | x<a+1 | B. | x<b+1 | C. | b+1<x<a+1 | D. | b<x<a |
14.已知等边△ABC中,A(-1,0),B(5,0),则点C的坐标为( )
| A. | (2,3$\sqrt{3}$) | B. | (2,-3$\sqrt{3}$) | C. | (3$\sqrt{3}$,2) | D. | (2,3$\sqrt{3}$)或(2,-3$\sqrt{3}$) |
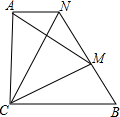 如图,点M在BN上,△ACM、△CBN是等边三角形,试证明:(1)AN=BM;(2)AN+MN=CN;(3)AN∥BC.
如图,点M在BN上,△ACM、△CBN是等边三角形,试证明:(1)AN=BM;(2)AN+MN=CN;(3)AN∥BC.