题目内容
7.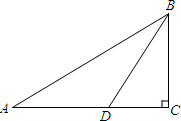 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,tan A=$\frac{\sqrt{3}}{3}$,AD=20.求BC的长.
如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,tan A=$\frac{\sqrt{3}}{3}$,AD=20.求BC的长.
分析 根据在Rt△ABC中,∠C=90°,BD平分∠ABC,tan A=$\frac{\sqrt{3}}{3}$,AD=20,可以得到∠A的度数,从而可以得到∠ABC以及∠ABD和∠CBD的度数,由AD的长度可以得到BD、CD的长,从而可以求得BC的长.
解答 解:∵tan A=$\frac{\sqrt{3}}{3}$,
∴∠A=30°,
∴∠ABC=60°,
又∵BD平分∠ABC,AD=20,
∴∠A=∠ABD=∠CBD=30°,
∴AD=BD=20,
∴DC=10,
即AC=AD+DC=30,
又∵tan A=$\frac{BC}{AC}$,
∴BC=AC•tan A=30×$\frac{\sqrt{3}}{3}$=10$\sqrt{3}$.
即BC的长为10$\sqrt{3}$.
点评 本题考查解直角三角形,解题的关键是找出各个角和各条边之间的关系.

练习册系列答案
相关题目
18.下列各数中,为负数的是( )
| A. | 0 | B. | -3 | C. | 2 | D. | $\frac{1}{2}$ |
19.下列图形中不一定是轴对称图形的是( )
| A. | 角 | B. | 平行四边形 | C. | 等腰三角形 | D. | 正方形 |
16.若a>b,则不等式组$\left\{\begin{array}{l}{x<a+1}\\{x<b+1}\end{array}\right.$的解集是( )
| A. | x<a+1 | B. | x<b+1 | C. | b+1<x<a+1 | D. | b<x<a |