题目内容
11.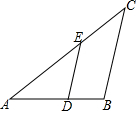 如图,已知△ABC∽△ADE,AE=5cm,EC=3cm,BC=6cm,∠BAC=∠C=40°.
如图,已知△ABC∽△ADE,AE=5cm,EC=3cm,BC=6cm,∠BAC=∠C=40°.(1)求∠AED和∠ADE的大小;
(2)求DE的长.
分析 (1)由△ABC∽△ADE可知:∠AED=∠C,由∠BAC=∠C可知∠AED=∠BAC
(2)由△ABC∽△ADE可知:$\frac{AE}{AC}=\frac{DE}{BC}$,将相关数据代入即可求出DE的长度.
解答 解:(1)由△ABC∽△ADE可知:∠AED=∠C,
∵∠BAC=∠C
∴∠AED=∠BAC=40°
∴∠ADE=180°-∠BAC-∠AED=100°
(2)由△ABC∽△ADE可知:$\frac{AE}{AC}=\frac{DE}{BC}$,
∴$\frac{5}{8}$=$\frac{DE}{6}$,
∴DE=$\frac{15}{4}$
点评 本题考查相似三角形的性质,解题的关键是熟练运用相似三角形的性质,本题属于基础题型.

练习册系列答案
相关题目
16.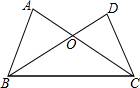 如图,下列条件中,不能证明△ABC≌△DCB的是( )
如图,下列条件中,不能证明△ABC≌△DCB的是( )
 如图,下列条件中,不能证明△ABC≌△DCB的是( )
如图,下列条件中,不能证明△ABC≌△DCB的是( )| A. | AB=DC,AC=DB | B. | AB=DC,∠ABC=∠DCB | C. | AC=BD,∠A=∠D | D. | BO=CO,∠A=∠D |
20.若关于x的二次函数y=mx2-2x+1的图象与x轴仅有一个公共点,则实数m=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 0或1 |

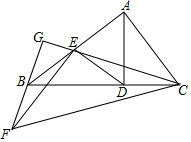 如图,Rt△ABC中,∠BAC=90°,过点A作AD⊥BC于点D,点E为线段AB中点,连接ED,EC将△EDC绕点E旋转,使点D和点B重合,得到△EBF,延长FB、CE相交于点G,若BC=$\sqrt{5}$,则BG=$\frac{\sqrt{5}}{3}$.
如图,Rt△ABC中,∠BAC=90°,过点A作AD⊥BC于点D,点E为线段AB中点,连接ED,EC将△EDC绕点E旋转,使点D和点B重合,得到△EBF,延长FB、CE相交于点G,若BC=$\sqrt{5}$,则BG=$\frac{\sqrt{5}}{3}$.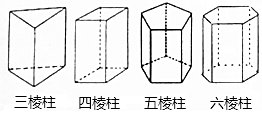 如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.
如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空. 如图,已知线段及∠M,只用直尺和圆规,求作△ABC,使BC=a,∠B=∠M,∠C=2∠M(保留作图痕迹,不写作法)
如图,已知线段及∠M,只用直尺和圆规,求作△ABC,使BC=a,∠B=∠M,∠C=2∠M(保留作图痕迹,不写作法)