题目内容
6.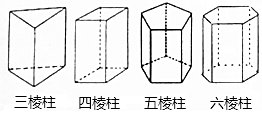 如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.
如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.(1)四棱柱有6个面,12条棱,8个顶点;
(2)六棱柱有8个面,18条棱,12个顶点;
(3)由此猜想n棱柱有(n+2)个面,3n条棱,2n个顶点.
分析 结合已知三棱柱、四棱柱、五棱柱和六棱柱的特点,可知n棱柱一定有(n+2)个面,3n条棱和2n个顶点.
解答 解:(1)四棱柱有6个面,12条棱,8个顶点;
(2)六棱柱有8个面,18条棱,12个顶点;
(3)由此猜想n棱柱有(n+2)个面,3n条棱,2n个顶点.
故答案为:(1)6,12,8;(2)8,18,12;(3)(n+2),3n,2n.
点评 此题考查了认识立体图形,熟记常见棱柱的特征,可以总结一般规律:n棱柱有(n+2)个面,3n条棱和2n个顶点.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
17.如果反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点(-3,2),则它一定还经过( )
| A. | (-$\frac{1}{2}$,8) | B. | (-3,-2) | C. | ($\frac{1}{2}$,12) | D. | (1,-6) |
14.已知线段AB=6,若点C到点A距离为2,到点B的距离为3,则对点C描述正确的是( )
| A. | 在线段AB所在的平面内能找到无数多个这样的点C | |
| B. | 满足条件的点C都在线段AB上 | |
| C. | 满足条件的点C都在两条射线上 | |
| D. | 这样的点C不存在 |
18.若(x+2)有平方根,则x的取值范围是( )
| A. | x<-2 | B. | x≤-2 | C. | x>2 | D. | x≥-2 |
15.已知⊙O的半径为4,点P到点O的距离为3,则点P与⊙O的位置关系是( )
| A. | 在圆内 | B. | 在圆上 | C. | 在圆外 | D. | 不确定 |
16.下列各式结果为负数的是( )
| A. | -(-1) | B. | -|-1| | C. | (-1)4 | D. | |1-2| |
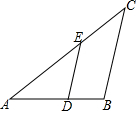 如图,已知△ABC∽△ADE,AE=5cm,EC=3cm,BC=6cm,∠BAC=∠C=40°.
如图,已知△ABC∽△ADE,AE=5cm,EC=3cm,BC=6cm,∠BAC=∠C=40°.