题目内容
20．若关于x的二次函数y=mx2-2x+1的图象与x轴仅有一个公共点，则实数m=（ ）| A． | -1 | B． | 0 | C． | 1 | D． | 0或1 |
分析 m≠0，则函数为二次函数．由抛物线与x轴只有一个交点，得到根的判别式的值等于0，且m不为0，即可求出m的值．
解答 解：∵二次函数y=mx2-2x+1的图象与x轴只有一个公共点，
∴△=4-4m=0，且m≠0，
解得 m=1．
故选C．
点评 此题考查了一次函数的性质与抛物线与x轴的交点，关键是掌握抛物线与x轴的交点个数由根的判别式的值来确定．本题中函数是二次函数，则二次项系数不等于零．
练习册系列答案
相关题目
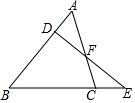如图，已知△ABC的边AB上有一点D，边BC的延长线上有一点E，且AD=CE．DE交AC于点F，试证明：AB•DF=BC•EF．
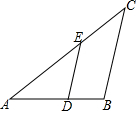如图，已知△ABC∽△ADE，AE=5cm，EC=3cm，BC=6cm，∠BAC=∠C=40°．
如图，在Rt△ABC中，AC=BC，∠ACB=90°，AD平分∠BAC，BE⊥AD交AC的延长线于点F，E为垂足，则结论：：①AD=BF；②CF=CD；③AC+CD=AB；④BE=CF；⑤BF=2BE，其中正确结论的个数是（ ）
15．已知⊙O的半径为4，点P到点O的距离为3，则点P与⊙O的位置关系是（ ）
| A． | 在圆内 | B． | 在圆上 | C． | 在圆外 | D． | 不确定 |
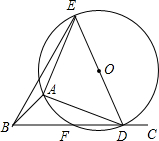如图，∠ABC=45°，△ADE是等腰直角三角形，AE=AD，顶点A，D分别在∠ABC的两边BA，BC上滑动（不与点B重合），△ADE的外接圆交BC于点F，O为圆心．
12．下列式子去括号正确的是（ ）
| A． | -（2a-b）=-2a-b | B． | 3a+（4a2+2）=3a+4a2-2 | ||
| C． | -（2a+3y）=2a-3y | D． | -2（a-6）=-2a+12 |